1. Introduction
In Geometric invariant theory (GIT), when constructing moduli spaces one typically focuses on those varieties that are asymptotically Chow semistable [Reference Mumford, Fogarty and KirwanMFK94, Reference Gelfand, Kapranov and ZelevinskyGKZ94]. Chow stability has many relations with other stabilities in Kähler geometry (see [Reference Ross and ThomasRT07, Reference YotsutaniYot17] for example), so it is important to study the Chow stability of singular varieties. However, unlike the smooth case, which is related to the constant scalar curvature (cscK) manifolds ([Reference DonaldsonDon01, Reference MabuchiMab04, Reference MabuchiMab06, Reference Ross and ThomasRT07]; see also the survey paper [Reference Phong and SturmPS10] for example), in general, K stability or the existence of cscK cannot imply Chow stability. Moreover, there are few examples of Chow polystable singular varieties. In general, it is very difficult to show that a variety is asymptotically Chow semistable. However, by the work of Futaki [Reference FutakiFut04] and Ono [Reference OnoOno13], we can determine the asymptotic Chow polystability of toric varieties. We first recall the main theorem we used in [Reference OnoOno13] (see also [Reference Lee, Li, Sturm and WangLLSW19]).
Theorem 1.1 ([Reference OnoOno13]). Let
![]() $P$
be an integral convex polytope of an n-dimensional toric variety
$P$
be an integral convex polytope of an n-dimensional toric variety
![]() $X_P$
, and let
$X_P$
, and let
![]() $G\lt SL(n,\mathbb {Z})$
be the biggest finite group acting on
$G\lt SL(n,\mathbb {Z})$
be the biggest finite group acting on
![]() $P$
by multiplication. Then
$P$
by multiplication. Then
![]() $X_P$
is asymptotically Chow semistable if and only if for any
$X_P$
is asymptotically Chow semistable if and only if for any
![]() $k\in \mathbb {N}$
, and for any convex
$k\in \mathbb {N}$
, and for any convex
![]() $G$
invariant function
$G$
invariant function
![]() $f$
on
$f$
on
![]() $kP$
, we have
$kP$
, we have
As a remark, in the original literature, Ono used concave functions instead of convex functions, so the direction of inequality in this note is different.
In this note, we mainly focus on symmetric reflexive toric varieties. One of the reasons is inspired by [Reference Batyrev and SelivanovaBS99], which shows that if a polytope is symmetric and reflexive, then it admits a Kähler–Einstein metric. With the result of [Reference DonaldsonDon02], we can see that symmetric and reflexive implies K stability. So it is natural to ask if it is true for Chow stability. The second reason is that, in this note, we define an invariant called Futaki–Ono invariant, which is
 \begin{equation*}FO_P(a,k):=\frac {1}{\chi (kP \cap \mathbb {Z}^n)} \sum _{k p\in kP \cap \mathbb {Z}^n} a(p)-\frac {1}{\textrm{Vol}(P)}\int _P a(x)\, dV.\end{equation*}
\begin{equation*}FO_P(a,k):=\frac {1}{\chi (kP \cap \mathbb {Z}^n)} \sum _{k p\in kP \cap \mathbb {Z}^n} a(p)-\frac {1}{\textrm{Vol}(P)}\int _P a(x)\, dV.\end{equation*}
As a rephrasing of Corollary 4.7 in [Reference OnoOno13], we can see that if
![]() $P$
is asymptotically Chow semistable, then this invariant will vanish for all
$P$
is asymptotically Chow semistable, then this invariant will vanish for all
![]() $k\gt \gt k_0$
and for all affine functions
$k\gt \gt k_0$
and for all affine functions
![]() $a$
. We can see that symmetric polytopes satisfy this criterion, so it is natural to study symmetric polytopes. Also, by Claim 4.3 in [Reference Lee, Li, Sturm and WangLLSW19], there is an example in which a symmetric non-reflexive polytope is not asymptotic Chow semistable. On the other hand, by the results in [Reference Lee, Li, Sturm and WangLLSW19], with the fact that
$a$
. We can see that symmetric polytopes satisfy this criterion, so it is natural to study symmetric polytopes. Also, by Claim 4.3 in [Reference Lee, Li, Sturm and WangLLSW19], there is an example in which a symmetric non-reflexive polytope is not asymptotic Chow semistable. On the other hand, by the results in [Reference Lee, Li, Sturm and WangLLSW19], with the fact that
![]() $\mathbb {P}^2$
and
$\mathbb {P}^2$
and
![]() $\mathbb {P}^1 \times \mathbb {P}^1$
are asymptotic Chow polystable, we can see that all two-dimensional symmetric reflexive toric varieties are asymptotically Chow polystable. So it is natural to study symmetric reflexive polytopes.
$\mathbb {P}^1 \times \mathbb {P}^1$
are asymptotic Chow polystable, we can see that all two-dimensional symmetric reflexive toric varieties are asymptotically Chow polystable. So it is natural to study symmetric reflexive polytopes.
However, a toric variety being symmetric and reflexive is generally not enough to guarantee that it is asymptotically Chow semistable, as illustrated by Example 3.9. Notice that this is not an isolated example. Indeed we can construct many examples using Proposition 3.7.
Therefore, to ensure asymptotic Chow polystability holds, one need more conditions on symmetric reflexive polytopes. One of the sufficient conditions is given by the following.
Definition 1.2 (See Definition 4.3 for the details). Let
![]() $P$
be an n-dimensional integral convex polytope on
$P$
be an n-dimensional integral convex polytope on
![]() $\mathbb {R}^n$
. We say
$\mathbb {R}^n$
. We say
![]() $P$
has regular boundary if for any
$P$
has regular boundary if for any
![]() $k\in \mathbb {N}$
, there exists a triangulation of
$k\in \mathbb {N}$
, there exists a triangulation of
![]() $\partial kP$
which every ‘triangle’ is integrally isomorphic to
$\partial kP$
which every ‘triangle’ is integrally isomorphic to
the standard
![]() $(n-1)$
-dimensional simplex (i.e. the intersection between different
$(n-1)$
-dimensional simplex (i.e. the intersection between different
![]() $T_{n-1}^i$
are at the boundary) such that:
$T_{n-1}^i$
are at the boundary) such that:
-
(i) for any point
 $p\in \partial kP$
, the number of simplices intersects with
$p\in \partial kP$
, the number of simplices intersects with
 $p$
, denoted as
$p$
, denoted as
 $m_k(p)$
, is bounded by
$m_k(p)$
, is bounded by
 $n!$
(i.e.
$n!$
(i.e.
 $m_k(p)\leqslant n!$
); and
$m_k(p)\leqslant n!$
); and -
(ii) this is the sub-triangulation of each face.
Here, integrally isomorphic means one of the objects is obtained from another object by an integral rigid motion, i.e. the multiplication of a matrix
![]() $A\in SL(n, \mathbb {Z})$
and translation of
$A\in SL(n, \mathbb {Z})$
and translation of
![]() $v\in \mathbb {Z}^{n}$
.
$v\in \mathbb {Z}^{n}$
.
We also make the following definition.
Definition 1.3 (See Definition 4.5 for the details). An integral convex polytope on
![]() $\mathbb {R}^n$
is called special if it is reflexive, weakly symmetric, and has a regular boundary.
$\mathbb {R}^n$
is called special if it is reflexive, weakly symmetric, and has a regular boundary.
One of our main theorems is given as follows.
Theorem 1.4 (See Theorem 6.1 for the details). Let
![]() $P$
be a special polytope. Then
$P$
be a special polytope. Then
![]() $P$
is asymptotically Chow polystable.
$P$
is asymptotically Chow polystable.
Notice that this condition is not necessary, as Theorem 8.1 gives another sufficient criterion to show when a toric variety
![]() $P$
is asymptotically Chow polystable. The statement of the theorem is the following.
$P$
is asymptotically Chow polystable. The statement of the theorem is the following.
Theorem 1.5 (See Theorem 8.1 for the details). Let
![]() $P$
be an integral polytope with
$P$
be an integral polytope with
![]() $0\in P^0$
such that all the Futaki–Ono invariants vanish, and one has a triangulation on
$0\in P^0$
such that all the Futaki–Ono invariants vanish, and one has a triangulation on
![]() $kP$
by
$kP$
by
![]() $n$
simplices, and a triangulation on
$n$
simplices, and a triangulation on
![]() $\partial kP$
by
$\partial kP$
by
![]() $(n-1)$
simplices. We let
$(n-1)$
simplices. We let
![]() $n(p;k)$
be the number of
$n(p;k)$
be the number of
![]() $n$
simplices attached to
$n$
simplices attached to
![]() $p\in kP$
in the first triangulation, and
$p\in kP$
in the first triangulation, and
![]() $m(p;k)$
be the number of
$m(p;k)$
be the number of
![]() $(n-1)$
simplices attached to
$(n-1)$
simplices attached to
![]() $p\in \partial kP$
in the second. Suppose
$p\in \partial kP$
in the second. Suppose
![]() $n(p;k)\leqslant (n+1)!$
for all
$n(p;k)\leqslant (n+1)!$
for all
![]() $p\neq 0$
, and
$p\neq 0$
, and
for all
![]() $k\gt \gt 0$
and for all
$k\gt \gt 0$
and for all
![]() $p\in \partial kP$
. Then
$p\in \partial kP$
. Then
![]() $P$
is asymptotically Chow polystable.
$P$
is asymptotically Chow polystable.
As a concrete example, we have the following corollary.
Corollary 1.6 (See Corollary 8.4 for the details).
![]() $D(X_8)$
and
$D(X_8)$
and
![]() $D(X_9)$
are asymptotically Chow polystable, where
$D(X_9)$
are asymptotically Chow polystable, where
![]() $D(X_8)$
and
$D(X_8)$
and
![]() $D(X_9)$
are defined in Example 4.8
.
$D(X_9)$
are defined in Example 4.8
.
This example shows that there are non-special symmetric reflexive polytopes that are asymptotically Chow polystable.
In the last section, we provide examples which are asymptotically Chow polystable, mainly of dimension 3, and have two classes of examples for higher dimensions. Notice that besides
![]() $D(X_8)$
and
$D(X_8)$
and
![]() $D(X_9)$
, the remaining examples are special. Also, the corresponding varieties of the examples are given in the Appendix.
$D(X_9)$
, the remaining examples are special. Also, the corresponding varieties of the examples are given in the Appendix.
2. Chow stability of toric varieties and criteria
2.1 GIT and Chow stabilities
In this section, we briefly recall some basic knowledge of GIT. For details, please read [Reference Gelfand, Kapranov and ZelevinskyGKZ94].
Definition 2.1. Let
![]() $G$
be a reductive algebraic group and
$G$
be a reductive algebraic group and
![]() $V$
be a finite-dimensional complex vector space such that
$V$
be a finite-dimensional complex vector space such that
![]() $G$
acts linearly on
$G$
acts linearly on
![]() $V$
. Let
$V$
. Let
![]() $v\neq 0 \in V$
, and let
$v\neq 0 \in V$
, and let
![]() $\mathcal {O}_G(v)$
be the
$\mathcal {O}_G(v)$
be the
![]() $G$
-orbit in
$G$
-orbit in
![]() $V$
. Then:
$V$
. Then:
-
(i)
 $v$
is called
$v$
is called
 $G$
-semistable if the Zariski closure of
$G$
-semistable if the Zariski closure of
 $\mathcal O_G(v)$
does not contain the origin, i.e.
$\mathcal O_G(v)$
does not contain the origin, i.e.
 $0\notin \overline {\mathcal O_G(v)}$
;
$0\notin \overline {\mathcal O_G(v)}$
; -
(ii)
 $v$
is called
$v$
is called
 $G$
-polystable if
$G$
-polystable if
 $0\notin \mathcal {O}_G(v)$
is a closed orbit;
$0\notin \mathcal {O}_G(v)$
is a closed orbit; -
(iii)
 $v$
is called
$v$
is called
 $G$
-stable if
$G$
-stable if
 $v$
is
$v$
is
 $G$
-polystable and Stabilizer of
$G$
-polystable and Stabilizer of
 $v$
,
$v$
,
 $G_v$
, is a finite group.
$G_v$
, is a finite group.
It is said that
![]() $[v]\in \mathbb {P}(V)$
is
$[v]\in \mathbb {P}(V)$
is
![]() $G$
-polystable (respectively, semistable) if
$G$
-polystable (respectively, semistable) if
![]() $v\in V$
is
$v\in V$
is
![]() $G$
-polystable (respectively, semistable).
$G$
-polystable (respectively, semistable).
Let
![]() $(X,L)$
be an
$(X,L)$
be an
![]() $n$
-dimensional polarized variety of degree
$n$
-dimensional polarized variety of degree
![]() $d$
, i.e.
$d$
, i.e.
![]() $X$
is a complex irreducible variety with degree
$X$
is a complex irreducible variety with degree
![]() $d$
, and
$d$
, and
![]() $L$
is an ample line bundle. Then there exists
$L$
is an ample line bundle. Then there exists
![]() $k_0\in \mathbb {N}$
such that, for every integer
$k_0\in \mathbb {N}$
such that, for every integer
![]() $k\geqslant k_0$
, there exists an embedding map
$k\geqslant k_0$
, there exists an embedding map
![]() $\iota _k\colon X\rightarrow \mathbb {P}(H^0(X,kL))\cong \mathbb {P}^{N_k}$
defined by
$\iota _k\colon X\rightarrow \mathbb {P}(H^0(X,kL))\cong \mathbb {P}^{N_k}$
defined by
where
![]() $\{s_0,\cdots, s_{N_k}\}$
is a basis of
$\{s_0,\cdots, s_{N_k}\}$
is a basis of
![]() $H^0(X,kL)$
. Consider
$H^0(X,kL)$
. Consider
![]() $\underline {\iota _k(X)}$
be the corresponding image on
$\underline {\iota _k(X)}$
be the corresponding image on
![]() $H^0(X,kL)$
, i.e.
$H^0(X,kL)$
, i.e.
![]() $p\in \underline {\iota _k(X)}$
if and only if
$p\in \underline {\iota _k(X)}$
if and only if
![]() $[p]\in \iota _k(X)$
. Then
$[p]\in \iota _k(X)$
. Then
![]() $\underline {\iota _k(X)}$
is an
$\underline {\iota _k(X)}$
is an
![]() $(n+1)$
-dimensional cone in
$(n+1)$
-dimensional cone in
![]() $H^0(X,kL)\cong {\mathbb {C}}^{N_k+1}$
. Then, for a generic linear
$H^0(X,kL)\cong {\mathbb {C}}^{N_k+1}$
. Then, for a generic linear
![]() $N_k-n+1$
subspace
$N_k-n+1$
subspace
![]() $W\subset H^0(X,kL)$
, the set of intersections between
$W\subset H^0(X,kL)$
, the set of intersections between
![]() $W$
and
$W$
and
![]() $\underline {\iota _k(X)}$
is in dimension 1, but for a generic linear
$\underline {\iota _k(X)}$
is in dimension 1, but for a generic linear
![]() $N_k-n$
subspace
$N_k-n$
subspace
![]() $L\subset H^0(X,kL)$
, the set of intersections between
$L\subset H^0(X,kL)$
, the set of intersections between
![]() $L$
and
$L$
and
![]() $\underline {\iota _k(X)}$
is
$\underline {\iota _k(X)}$
is
![]() $\{0\}$
.
$\{0\}$
.
Therefore, we can define a degree
![]() $d$
divisor
$d$
divisor
![]() $Z_X$
on the Grassmannian
$Z_X$
on the Grassmannian
![]() $Gr(N_k-n, N_k+1)$
by
$Gr(N_k-n, N_k+1)$
by
This induces a point
![]() $R_X\in \mathbb {P}(H^0(Gr(N_k-n, N_k+1)), \mathcal {O}(d))$
, which is called the Chow point.
$R_X\in \mathbb {P}(H^0(Gr(N_k-n, N_k+1)), \mathcal {O}(d))$
, which is called the Chow point.
Also, under the embedding
![]() $Gr(N_k-n, N_k+1)\rightarrow \wedge ^{n+1}(H^0(X,kL))$
, where
$Gr(N_k-n, N_k+1)\rightarrow \wedge ^{n+1}(H^0(X,kL))$
, where
![]() $V=H^0(X,kL)$
, we have
$V=H^0(X,kL)$
, we have
and then the
![]() $SL(N_k+1,{\mathbb {C}})$
action on
$SL(N_k+1,{\mathbb {C}})$
action on
![]() $H^0(X,kL)$
induces an action on
$H^0(X,kL)$
induces an action on
![]() $V_k$
.
$V_k$
.
Definition 2.2. We say that:
-
(i)
 $X$
is
$X$
is
 $k$
Chow stable (respectively, polystable, semistable) if
$k$
Chow stable (respectively, polystable, semistable) if
 $R_X\in V_k$
is
$R_X\in V_k$
is
 $SL(N_k+1,{\mathbb {C}})$
-stable (respectively,
$SL(N_k+1,{\mathbb {C}})$
-stable (respectively,
 $SL(N_k+1,{\mathbb {C}})$
-polystable,
$SL(N_k+1,{\mathbb {C}})$
-polystable,
 $SL(N_k+1,{\mathbb {C}})$
- semistable); and
$SL(N_k+1,{\mathbb {C}})$
- semistable); and -
(ii)
 $X$
is asymptotically Chow stable (respectively, polystable, semistable) if there exists
$X$
is asymptotically Chow stable (respectively, polystable, semistable) if there exists
 $k_0$
such that
$k_0$
such that
 $X$
is
$X$
is
 $k$
Chow stable (respectively, polystable, semistable) for all
$k$
Chow stable (respectively, polystable, semistable) for all
 $k\geqslant k_0$
.
$k\geqslant k_0$
.
2.2 Toric varieties
We now recall some background knowledge of toric varieties.
Definition 2.3. Let
![]() $X$
be an
$X$
be an
![]() $n$
-dimensional algebraic variety. Then
$n$
-dimensional algebraic variety. Then
![]() $X$
is a toric variety if:
$X$
is a toric variety if:
-
(i)
 $X$
is a Zaraki closure of
$X$
is a Zaraki closure of
 $({\mathbb {C}}^*)^n$
;
$({\mathbb {C}}^*)^n$
; -
(ii) the left multiplication of
 $({\mathbb {C}}^*)^n$
on
$({\mathbb {C}}^*)^n$
on
 $({\mathbb {C}}^*)^n$
can extend to an action on
$({\mathbb {C}}^*)^n$
can extend to an action on
 $X$
.
$X$
.
We will focus on polarized toric varieties
![]() $(X,L)$
. There exists
$(X,L)$
. There exists
![]() $k_0$
such that for all
$k_0$
such that for all
![]() $k\geqslant k_0$
, the map
$k\geqslant k_0$
, the map
![]() $\iota _k\colon X \rightarrow \mathbb {P}(H^0(X,kL))$
we defined above is embedding. Moreover, we can choose the basis
$\iota _k\colon X \rightarrow \mathbb {P}(H^0(X,kL))$
we defined above is embedding. Moreover, we can choose the basis
![]() $\{s_0,\ldots, s_{N_k}\}$
such that for any
$\{s_0,\ldots, s_{N_k}\}$
such that for any
![]() $\lambda :=(e^{\lambda _1},\ldots, e^{\lambda _n})\in ({\mathbb {C}}^*)^n$
,
$\lambda :=(e^{\lambda _1},\ldots, e^{\lambda _n})\in ({\mathbb {C}}^*)^n$
,
Then for
![]() $\lambda \in ({\mathbb {C}}^*)^n$
,
$\lambda \in ({\mathbb {C}}^*)^n$
,
and, in particular, the
![]() $(S^1)^n\lt ({\mathbb {C}}^*)^n$
is a subgroup of the Hamiltonian group of
$(S^1)^n\lt ({\mathbb {C}}^*)^n$
is a subgroup of the Hamiltonian group of
![]() $\iota _k^*\omega _{FS}$
. Thus we have the moment polytopes
$\iota _k^*\omega _{FS}$
. Thus we have the moment polytopes
![]() $\mu _k\colon X \rightarrow \textrm{Lie}((S^1)^n)\cong \mathbb {R}^n$
, and the images are defined as the moment map polytope
$\mu _k\colon X \rightarrow \textrm{Lie}((S^1)^n)\cong \mathbb {R}^n$
, and the images are defined as the moment map polytope
![]() $P_k$
. Notice that we have
$P_k$
. Notice that we have
if
![]() $\iota _k$
defines an embedding. Moreover,
$\iota _k$
defines an embedding. Moreover,
The reason is we have a moment map
![]() $\mu _{\mathbb {P}^{N_k}}\colon \mathbb {P}^{N_k}\rightarrow \textrm{Lie}((S^1)^{N_k})^*$
, and the image is the standard simplex. Then the moment map
$\mu _{\mathbb {P}^{N_k}}\colon \mathbb {P}^{N_k}\rightarrow \textrm{Lie}((S^1)^{N_k})^*$
, and the image is the standard simplex. Then the moment map
where
is the induced homomorphism from
![]() $\iota _k$
,
$\iota _k$
,
In terms of a matrix,
 \begin{align*}(\iota _k)_*=\left(\begin{matrix} \alpha _0^1 & & \cdots & & \alpha _0^n \\[3pt]\vdots & & \ddots & & \vdots \\[3pt] \alpha _{N_k}^1 & & \cdots & & \alpha _{N_k}^n \end{matrix}\right),\end{align*}
\begin{align*}(\iota _k)_*=\left(\begin{matrix} \alpha _0^1 & & \cdots & & \alpha _0^n \\[3pt]\vdots & & \ddots & & \vdots \\[3pt] \alpha _{N_k}^1 & & \cdots & & \alpha _{N_k}^n \end{matrix}\right),\end{align*}
and as a result,
![]() $\iota _k^*=((\iota _k)_*)^T$
is the transpose and therefore
$\iota _k^*=((\iota _k)_*)^T$
is the transpose and therefore
Definition 2.4. Let
![]() $(X,L)$
be a polarized toric variety such that
$(X,L)$
be a polarized toric variety such that
![]() $\iota\colon X \rightarrow \mathbb {P}(H^0(X,L))$
is the toric equivariant Kodaira embedding map, and let
$\iota\colon X \rightarrow \mathbb {P}(H^0(X,L))$
is the toric equivariant Kodaira embedding map, and let
![]() $P$
be the corresponding polytope. Then
$P$
be the corresponding polytope. Then
![]() $P$
is said to be asymptotically Chow stable (respectively, polystable, semistable) if
$P$
is said to be asymptotically Chow stable (respectively, polystable, semistable) if
![]() $(X,L)$
is asymptotically Chow stable (respectively, polystable, semistable).
$(X,L)$
is asymptotically Chow stable (respectively, polystable, semistable).
2.3 Chow stability of toric variety and criteria
Recall that by Fataki and Ono ([Reference FutakiFut04, Reference OnoOno13, Reference Ono, Sano and YotsutaniOSY12], and also see [Reference Lee, Li, Sturm and WangLLSW19]), a toric variety
![]() $X_P$
is asymptotically Chow semistable if there exists
$X_P$
is asymptotically Chow semistable if there exists
![]() $C$
such that for any
$C$
such that for any
![]() $k\geqslant C$
, and for any convex
$k\geqslant C$
, and for any convex
![]() $G$
invariant function
$G$
invariant function
![]() $f\colon kP \rightarrow \mathbb {R}$
, we have
$f\colon kP \rightarrow \mathbb {R}$
, we have
 \begin{align} \frac {1}{\textrm{Vol}(kP)}\int _{kP} f\, dV\leqslant \frac {1}{\chi (kP \cap \mathbb {Z}^n)} \sum _{k p\in kP \cap \mathbb {Z}^n} f(p), \end{align}
\begin{align} \frac {1}{\textrm{Vol}(kP)}\int _{kP} f\, dV\leqslant \frac {1}{\chi (kP \cap \mathbb {Z}^n)} \sum _{k p\in kP \cap \mathbb {Z}^n} f(p), \end{align}
and
![]() $X_P$
is polystable if the equality holds only when
$X_P$
is polystable if the equality holds only when
![]() $v$
is affine. (In [Reference OnoOno13] and [Reference Lee, Li, Sturm and WangLLSW19], the inequality is on the opposite side as the inputs are concave functions.) Here
$v$
is affine. (In [Reference OnoOno13] and [Reference Lee, Li, Sturm and WangLLSW19], the inequality is on the opposite side as the inputs are concave functions.) Here
![]() $G\lt SL(n, \mathbb {Z})$
is the biggest group fixing
$G\lt SL(n, \mathbb {Z})$
is the biggest group fixing
![]() $P$
, which is a discrete group.
$P$
, which is a discrete group.
Notice that if there exists a toric equivariant
![]() ${\mathbb {C}}^*$
action on
${\mathbb {C}}^*$
action on
![]() $X_P$
, then it corresponds to an affine function on
$X_P$
, then it corresponds to an affine function on
![]() $P$
(see [Reference DonaldsonDon02]). So we can write the following definition.
$P$
(see [Reference DonaldsonDon02]). So we can write the following definition.
Definition 2.5. Let
![]() $P$
be an integral convex polytope. The Futaki–Ono invariant of an affine function
$P$
be an integral convex polytope. The Futaki–Ono invariant of an affine function
![]() $v(x)=a_1x_1+\cdots +a_nx_n+a_0$
is given by
$v(x)=a_1x_1+\cdots +a_nx_n+a_0$
is given by
 \begin{equation*}FO_P(a,k):=\frac {1}{\chi (kP \cap \mathbb {Z}^n)} \sum _{k p\in kP \cap \mathbb {Z}^n} a(p)-\frac {1}{\textrm{Vol}(P)}\int _P a(x)\, dV.\end{equation*}
\begin{equation*}FO_P(a,k):=\frac {1}{\chi (kP \cap \mathbb {Z}^n)} \sum _{k p\in kP \cap \mathbb {Z}^n} a(p)-\frac {1}{\textrm{Vol}(P)}\int _P a(x)\, dV.\end{equation*}
We can rephrase Corollary 4.7 in [Reference OnoOno13] as the following lemma.
Lemma 2.6 (Corollary 4.7 in [Reference OnoOno13]; also see [Reference FutakiFut04]). Suppose
![]() $P$
is asymptotically Chow semistable. Then there exists
$P$
is asymptotically Chow semistable. Then there exists
![]() $C$
such that for any
$C$
such that for any
![]() $k\geqslant C$
, and for any affine function
$k\geqslant C$
, and for any affine function
![]() $a$
on
$a$
on
![]() $kP$
, we have
$kP$
, we have
Recall the following definition.
Definition 2.7. An integral convex polytope
![]() $P$
is symmetric if there is exactly one fixed point (which must be 0 for reflexive polytopes) of the symmetric group
$P$
is symmetric if there is exactly one fixed point (which must be 0 for reflexive polytopes) of the symmetric group
![]() $G\lt SL(n, \mathbb {Z})$
acting on
$G\lt SL(n, \mathbb {Z})$
acting on
![]() $P$
.
$P$
.
In particular, any
![]() $G$
invariant affine function on symmetric polytopes must be constant; hence it must vanish. We also define the following.
$G$
invariant affine function on symmetric polytopes must be constant; hence it must vanish. We also define the following.
Definition 2.8. A polytope
![]() $P$
is weakly symmetric if for any
$P$
is weakly symmetric if for any
![]() $k$
, and for any affine function
$k$
, and for any affine function
![]() $a$
on
$a$
on
![]() $kP$
,
$kP$
,
Remark 2.9. Notice that this condition is stronger than assuming
![]() $FO_P(a,k)=0$
for all
$FO_P(a,k)=0$
for all
![]() $k\gt \gt 0$
. There are two questions that arise.
$k\gt \gt 0$
. There are two questions that arise.
-
(i) It is easy to see that
 $P$
is symmetric implies
$P$
is symmetric implies
 $P$
is weakly symmetric. But is the opposite true?
$P$
is weakly symmetric. But is the opposite true? -
(ii) If
 $P$
is not weakly symmetric, does this imply
$P$
is not weakly symmetric, does this imply
 $P$
is not asymptotically Chow semistable?
$P$
is not asymptotically Chow semistable?
Notice that the K stability version is not true, as there are non-symmetric K stable toric varieties, for example, the toric Del Pezzo surface of degree 1. However, it is not weakly symmetric and not asymptotically Chow semistable (see [Reference Lee, Li, Sturm and WangLLSW19], Section 5).
Lemma 2.10.
A weakly symmetric integral polytopes
![]() $P$
is (asymptotically ) Chow semistable if for any
$P$
is (asymptotically ) Chow semistable if for any
![]() $k\in \mathbb {N}$
(
$k\in \mathbb {N}$
(
![]() $k \geqslant C$
for some fix
$k \geqslant C$
for some fix
![]() $C$
), and for any convex function
$C$
), and for any convex function
![]() $f\colon kP\rightarrow \mathbb {R}$
which
$f\colon kP\rightarrow \mathbb {R}$
which
![]() $\min _{x\in kP}f(x)=f(0)=0$
, we have
$\min _{x\in kP}f(x)=f(0)=0$
, we have
Proof.
For any convex function
![]() $f\colon kP\rightarrow \mathbb {R}$
, there exists an affine function
$f\colon kP\rightarrow \mathbb {R}$
, there exists an affine function
![]() $a_k$
such that
$a_k$
such that
Therefore, we have
The result follows.
3. Some special classes of toric varieties
3.1 Product class
The first class of polytopes is in the form
![]() $P_1\times \cdots \times P_r$
, where
$P_1\times \cdots \times P_r$
, where
![]() $P_1,\ldots, P_r$
, and is Chow stable.
$P_1,\ldots, P_r$
, and is Chow stable.
Lemma 3.1.
Let
![]() $P_1$
and
$P_1$
and
![]() $P_2$
be bounded convex sets. Then for any
$P_2$
be bounded convex sets. Then for any
![]() $f$
which is a convex function on
$f$
which is a convex function on
![]() $P_1\times P_2$
,
$P_1\times P_2$
,
![]() $f_{P_2}(x):=\int _{P_2}f(x,y)dV_y$
is a convex function on
$f_{P_2}(x):=\int _{P_2}f(x,y)dV_y$
is a convex function on
![]() $P_1$
.
$P_1$
.
Proof.
Consider
![]() $f_{P_2}(tx_1+(1-t)x_2)$
, where
$f_{P_2}(tx_1+(1-t)x_2)$
, where
![]() $0\leqslant t\leqslant 1$
. We have
$0\leqslant t\leqslant 1$
. We have
 \begin{align*} f_{P_2}(tx_1+(1-t)x_2)=&\int _{P_2}f(tx_1+(1-t)x_2,y)dV_y\\ \leqslant &\int _{P_2}tf(tx_1,y)dV_y+\int _{P_2}f((1-t)x_2,y)dV_y\\ =& tf_{P_2}(x_1)+(1-t)f_{P_2}(x_2). \end{align*}
\begin{align*} f_{P_2}(tx_1+(1-t)x_2)=&\int _{P_2}f(tx_1+(1-t)x_2,y)dV_y\\ \leqslant &\int _{P_2}tf(tx_1,y)dV_y+\int _{P_2}f((1-t)x_2,y)dV_y\\ =& tf_{P_2}(x_1)+(1-t)f_{P_2}(x_2). \end{align*}
Proposition 3.2.
Let
![]() $P_1$
and
$P_1$
and
![]() $P_2$
be integral convex polytopes. Then
$P_2$
be integral convex polytopes. Then
![]() $P_1\times P_2$
is (asymptotic) Chow polystable (semistable) if and only if
$P_1\times P_2$
is (asymptotic) Chow polystable (semistable) if and only if
![]() $P_1$
and
$P_1$
and
![]() $P_2$
are (asymptotic) Chow polystable (semistable).
$P_2$
are (asymptotic) Chow polystable (semistable).
Proof.
Suppose for any
![]() $k\geqslant C_1$
and
$k\geqslant C_1$
and
![]() $k \geqslant C_2$
and for any convex function
$k \geqslant C_2$
and for any convex function
![]() $f_1, f_2$
on
$f_1, f_2$
on
![]() $P_1$
and
$P_1$
and
![]() $P_2$
, we have
$P_2$
, we have
 \begin{equation*}\frac {1}{\textrm{Vol}(kP_1)}\int _{kP_1}f_1(x)dV\leqslant \frac {1}{\chi (kP_1)}\sum _{p\in P_1}f_2(p);\end{equation*}
\begin{equation*}\frac {1}{\textrm{Vol}(kP_1)}\int _{kP_1}f_1(x)dV\leqslant \frac {1}{\chi (kP_1)}\sum _{p\in P_1}f_2(p);\end{equation*}
 \begin{equation*}\frac {1}{\textrm{Vol}(kP_2)}\int _{kP_2}f_2(x)dV\leqslant \frac {1}{\chi (kP_2)}\sum _{p\in P_2}f_2(p).\end{equation*}
\begin{equation*}\frac {1}{\textrm{Vol}(kP_2)}\int _{kP_2}f_2(x)dV\leqslant \frac {1}{\chi (kP_2)}\sum _{p\in P_2}f_2(p).\end{equation*}
Then for any
![]() $k\geqslant \max \{C_1,C_2\}$
, and for any convex function
$k\geqslant \max \{C_1,C_2\}$
, and for any convex function
![]() $f$
, we have
$f$
, we have
 \begin{eqnarray*} \frac {1}{\textrm{Vol}(kP_1\times kP_2)}\int _{kP_1\times kP_2}f(x,y)dV_xdV_y &=&\frac {1}{\textrm{Vol}(kP_1)}\int _{kP_1} \frac {1}{\textrm{Vol}(kV_2)}\int _{kP_2}f(x,y)dV_ydV_x\\ &=&\frac {1}{\textrm{Vol}(kP_1)}\int _{kP_1} \frac {1}{\textrm{Vol}(kV_2)} f_{kP_2}(x)dV_x \qquad (\text {Lemma 3.1})\\ &\leqslant &\frac {1}{\textrm{Vol}(kP_2)} \frac {1}{\chi (kP_1)}\sum _{p_1\in kP_1\cap \mathbb {Z}^{n_1}}f_{P_2}(p_1)\\ &=&\frac {1}{\chi (kP_1)}\sum _{p_1\in kP_1\cap \mathbb {Z}^{n_1}}\left (\frac {1}{\textrm{Vol}(kP_2)}\int _{kP_2}f(p_1,y)dV_y\right )\\ &\leqslant & \frac {1}{\chi (kP_1)}\sum _{p_1\in kP_1\cap \mathbb {Z}^{n_1}}\frac {1}{\chi (kP_2)}\sum _{p_2\in kP_2\cap \mathbb {Z}^{n_2}}f(p_1,p_2)\\ &=& \frac {1}{\chi (k(P_1\times P_2))}\sum _{p\in k(P_1\times P_2)\cap \mathbb {Z}^{n_1}\times \mathbb {Z}^{n_2}}f(p). \end{eqnarray*}
\begin{eqnarray*} \frac {1}{\textrm{Vol}(kP_1\times kP_2)}\int _{kP_1\times kP_2}f(x,y)dV_xdV_y &=&\frac {1}{\textrm{Vol}(kP_1)}\int _{kP_1} \frac {1}{\textrm{Vol}(kV_2)}\int _{kP_2}f(x,y)dV_ydV_x\\ &=&\frac {1}{\textrm{Vol}(kP_1)}\int _{kP_1} \frac {1}{\textrm{Vol}(kV_2)} f_{kP_2}(x)dV_x \qquad (\text {Lemma 3.1})\\ &\leqslant &\frac {1}{\textrm{Vol}(kP_2)} \frac {1}{\chi (kP_1)}\sum _{p_1\in kP_1\cap \mathbb {Z}^{n_1}}f_{P_2}(p_1)\\ &=&\frac {1}{\chi (kP_1)}\sum _{p_1\in kP_1\cap \mathbb {Z}^{n_1}}\left (\frac {1}{\textrm{Vol}(kP_2)}\int _{kP_2}f(p_1,y)dV_y\right )\\ &\leqslant & \frac {1}{\chi (kP_1)}\sum _{p_1\in kP_1\cap \mathbb {Z}^{n_1}}\frac {1}{\chi (kP_2)}\sum _{p_2\in kP_2\cap \mathbb {Z}^{n_2}}f(p_1,p_2)\\ &=& \frac {1}{\chi (k(P_1\times P_2))}\sum _{p\in k(P_1\times P_2)\cap \mathbb {Z}^{n_1}\times \mathbb {Z}^{n_2}}f(p). \end{eqnarray*}
In particular, if
![]() $C_1=C_2=1$
, then this inequality holds for any convex function and any
$C_1=C_2=1$
, then this inequality holds for any convex function and any
![]() $k$
.
$k$
.
For the opposite, without loss of generality, assume
![]() $P_1$
is unstable. Then there exists a sequence of convex functions
$P_1$
is unstable. Then there exists a sequence of convex functions
![]() $f_k$
on
$f_k$
on
![]() $kP_1$
such that for any
$kP_1$
such that for any
![]() $k\gt \gt 0$
,
$k\gt \gt 0$
,
 \begin{equation*}\frac {1}{\textrm{Vol}(kP_1)}\int _{kP_1}f_k(x)dV \geqslant \frac {1}{\chi (kP_1)}\sum _{p\in kP_1\cap \mathbb {Z}^{n_1}}f(p).\end{equation*}
\begin{equation*}\frac {1}{\textrm{Vol}(kP_1)}\int _{kP_1}f_k(x)dV \geqslant \frac {1}{\chi (kP_1)}\sum _{p\in kP_1\cap \mathbb {Z}^{n_1}}f(p).\end{equation*}
Define
![]() $f_k\colon kP_1\times kP_2\rightarrow \mathbb {R}$
such that
$f_k\colon kP_1\times kP_2\rightarrow \mathbb {R}$
such that
Then
 \begin{align*} &\frac {1}{\textrm{Vol}(kP_1\times kP_2)}\int _{kP_1\times kP_2}f_k(x,y)dV=\frac {1}{\textrm{Vol} (kP_1)} \int _{kP_1}f_k(x)dv \geqslant \frac {1}{\chi (kP_1)}\sum _{p\in kP_1\cap \mathbb {Z}^{n_1}}f_k(p)\\ \qquad =& \frac {1}{\chi (kP_1\times kP_2)}\sum _{p\in kP_1\cap \mathbb {Z}^{n_1}} \chi (kP_2)f_k(p)=\frac {1}{\chi (k(P_1\times P_2))}\sum _{p\in k(P_1\times P_2)\cap \mathbb {Z}^{n_1}\times \mathbb {Z}^{n_2}} f_k(p). \end{align*}
\begin{align*} &\frac {1}{\textrm{Vol}(kP_1\times kP_2)}\int _{kP_1\times kP_2}f_k(x,y)dV=\frac {1}{\textrm{Vol} (kP_1)} \int _{kP_1}f_k(x)dv \geqslant \frac {1}{\chi (kP_1)}\sum _{p\in kP_1\cap \mathbb {Z}^{n_1}}f_k(p)\\ \qquad =& \frac {1}{\chi (kP_1\times kP_2)}\sum _{p\in kP_1\cap \mathbb {Z}^{n_1}} \chi (kP_2)f_k(p)=\frac {1}{\chi (k(P_1\times P_2))}\sum _{p\in k(P_1\times P_2)\cap \mathbb {Z}^{n_1}\times \mathbb {Z}^{n_2}} f_k(p). \end{align*}
As a quick check, we have a computational proof of the following well-known fact.
Corollary 3.3.
The variety
![]() $((\mathbb {P}^1)^n, -K_{(\mathbb {P}^1)^n})$
is asymptotically Chow polystable.
$((\mathbb {P}^1)^n, -K_{(\mathbb {P}^1)^n})$
is asymptotically Chow polystable.
Proof. The polytope
![]() $[-1,1]$
is asymptotically Chow polystable. A direct consequence of Proposition 3.2 implies that
$[-1,1]$
is asymptotically Chow polystable. A direct consequence of Proposition 3.2 implies that
![]() $[-1,1]^n$
is asymptotically Chow polystable.
$[-1,1]^n$
is asymptotically Chow polystable.
3.2 Symmetric double cone type
We now consider a class of examples where the members are reflexive and symmetric, but not asymptotically Chow semistable. Also, it is arguably one of the simplest and yet non-trivial classes to study.
Definition 3.4. Let
![]() $P$
be an
$P$
be an
![]() $n$
-dimensional integral polytope. Then we define the double cone
$n$
-dimensional integral polytope. Then we define the double cone
Notice that
Lemma 3.5.
Suppose
![]() $P$
is symmetric. Then
$P$
is symmetric. Then
![]() $D(P)$
is symmetric.
$D(P)$
is symmetric.
Proof.
If
![]() $G$
acts on
$G$
acts on
![]() $P$
, then
$P$
, then
![]() $G\times \mathbb {Z}/ 2\mathbb {Z}$
acts on
$G\times \mathbb {Z}/ 2\mathbb {Z}$
acts on
![]() $D(P)$
by
$D(P)$
by
Hence if
![]() $P$
is symmetric, then
$P$
is symmetric, then
![]() $D(P)$
is symmetric.
$D(P)$
is symmetric.
To give a counterexample, first we have the following well-known fact.
Lemma 3.6 (See [Ehr77] or [Reference Beck, De Loera, Develin, Pfeifle and StanleyBDLD+05]). Let
![]() $P$
be a convex integral polytope with dim
$P$
be a convex integral polytope with dim
![]() $\geqslant 2$
. Then the number of points
$\geqslant 2$
. Then the number of points
where
![]() $p(k)$
is a polynomial in
$p(k)$
is a polynomial in
![]() $k$
of degree
$k$
of degree
![]() $n-2$
which depends on
$n-2$
which depends on
![]() $P$
only. For
$P$
only. For
![]() $n=1$
,
$n=1$
,
and for
![]() $n=2$
, we have the Pick theorem (see [Reference PickPic99]),
$n=2$
, we have the Pick theorem (see [Reference PickPic99]),
In particular, for
![]() $k\gt \gt 0$
,
$k\gt \gt 0$
,
Proposition 3.7.
Let
![]() $P$
be an
$P$
be an
![]() $n$
-dimensional integral polytope. Suppose
$n$
-dimensional integral polytope. Suppose
![]() $\textrm{Vol}(P)\geqslant$
$\textrm{Vol}(P)\geqslant$
![]() $(n+2)(n+1)$
, so then
$(n+2)(n+1)$
, so then
![]() $D(P)$
is not asymptotically Chow semistable.
$D(P)$
is not asymptotically Chow semistable.
Proof.
For
![]() $kD(P)$
, denote the point in
$kD(P)$
, denote the point in
![]() $kD(P)$
to be
$kD(P)$
to be
![]() $(p,q)$
, where
$(p,q)$
, where
![]() $p\in \mathbb {R}^n$
,
$p\in \mathbb {R}^n$
,
![]() $q\in \mathbb {R}$
. Consider the function
$q\in \mathbb {R}$
. Consider the function
Then
Let
![]() $\textrm{Vol}(P)= (n+2)(n+1)(1+\delta )$
for some
$\textrm{Vol}(P)= (n+2)(n+1)(1+\delta )$
for some
![]() $\delta \geqslant 0$
. Then
$\delta \geqslant 0$
. Then
 \begin{align*} &\int _{kD(P)} f(x)\, dV=2\int _{0}^1 t(1-t)^n\textrm{Vol}(P) dt=2\textrm{Vol}(P)\int _{0}^1 t^n(1-t)dt\\ =& 2\textrm{Vol}(P)\left (\frac {1}{n+1}-\frac {1}{n+2}\right ) = 2 \frac {\textrm{Vol}(P)}{(n+1)(n+2)}=2+2\delta, \end{align*}
\begin{align*} &\int _{kD(P)} f(x)\, dV=2\int _{0}^1 t(1-t)^n\textrm{Vol}(P) dt=2\textrm{Vol}(P)\int _{0}^1 t^n(1-t)dt\\ =& 2\textrm{Vol}(P)\left (\frac {1}{n+1}-\frac {1}{n+2}\right ) = 2 \frac {\textrm{Vol}(P)}{(n+1)(n+2)}=2+2\delta, \end{align*}
for some fix
![]() $\delta \gt 0$
. Therefore,
$\delta \gt 0$
. Therefore,
and
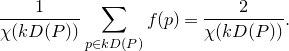 \begin{equation*} \frac {1}{\chi (kD(P))}\sum _{p\in kD(P)}f(p)=\frac {2}{\chi (kD(P))}.\end{equation*}
\begin{equation*} \frac {1}{\chi (kD(P))}\sum _{p\in kD(P)}f(p)=\frac {2}{\chi (kD(P))}.\end{equation*}
As a result,
 \begin{eqnarray*} \frac {1}{\chi (kD(P))}\sum _{p\in kD(P)}f(p)- \frac {1}{\textrm{Vol}(kD(P))}\int _{kD(P)} f(x)\, dV &=& \frac {2}{\chi (kD(P))}- \frac {2+2\delta }{\textrm{Vol}(kD(P))}\\ &\lt & \frac {2}{\textrm{Vol}(kD(P))}- \frac {2+2\delta }{\textrm{Vol}(kD(P))}\\ &=& \frac {-2\delta }{\textrm{Vol}(k D(P))}\\ &\leqslant & 0. \end{eqnarray*}
\begin{eqnarray*} \frac {1}{\chi (kD(P))}\sum _{p\in kD(P)}f(p)- \frac {1}{\textrm{Vol}(kD(P))}\int _{kD(P)} f(x)\, dV &=& \frac {2}{\chi (kD(P))}- \frac {2+2\delta }{\textrm{Vol}(kD(P))}\\ &\lt & \frac {2}{\textrm{Vol}(kD(P))}- \frac {2+2\delta }{\textrm{Vol}(kD(P))}\\ &=& \frac {-2\delta }{\textrm{Vol}(k D(P))}\\ &\leqslant & 0. \end{eqnarray*}
Example 3.8 (Claim 4.3 in [Reference Lee, Li, Sturm and WangLLSW19]). Let
![]() $P=[-a,a]$
for
$P=[-a,a]$
for
![]() $a\gt 3$
. Then
$a\gt 3$
. Then
![]() $D(P)$
is not asymptotically Chow semistable by the Proposition 3.7.
$D(P)$
is not asymptotically Chow semistable by the Proposition 3.7.
In the following example, we construct a toric variety which is defined by a reflexive and symmetric polytope, but it is not asymptotically Chow semistable.
Example 3.9.
Consider
![]() $P=[-1,1]^6= ((\mathbb {P}^1)^6, O(2,2,2,2,2,2))$
, so then
$P=[-1,1]^6= ((\mathbb {P}^1)^6, O(2,2,2,2,2,2))$
, so then
Indeed, as
![]() $2^x-(x+2)(x+1)$
is increasing when
$2^x-(x+2)(x+1)$
is increasing when
![]() $x\geqslant 6$
, so for all
$x\geqslant 6$
, so for all
![]() $n\geqslant 6$
,
$n\geqslant 6$
,
which implies that
![]() $D([-1,1]^n)$
are not asymptotically Chow semistable for all
$D([-1,1]^n)$
are not asymptotically Chow semistable for all
![]() $n\geqslant 6$
.
$n\geqslant 6$
.
Remark 3.10. In the previous example, we provided a sequence of functions
![]() $f_k\colon kD([-1,1]^n) \rightarrow \mathbb {R}$
such that the inequality (1) does not hold for all
$f_k\colon kD([-1,1]^n) \rightarrow \mathbb {R}$
such that the inequality (1) does not hold for all
![]() $k\gt \gt 0$
, and hence we show that
$k\gt \gt 0$
, and hence we show that
![]() $D([-1,1]^n)$
are not asymptotically Chow semistable for all
$D([-1,1]^n)$
are not asymptotically Chow semistable for all
![]() $n\geqslant 6$
. We can generalize this construction to any
$n\geqslant 6$
. We can generalize this construction to any
![]() $d$
-dimensional toric variety with the polytope
$d$
-dimensional toric variety with the polytope
![]() $\Delta$
. To be precise, for any
$\Delta$
. To be precise, for any
![]() $p\in \Delta$
, we define a sequence of piecewise linear functions
$p\in \Delta$
, we define a sequence of piecewise linear functions
![]() $f_{p,k}\colon k\Delta \rightarrow \mathbb {R}$
such that:
$f_{p,k}\colon k\Delta \rightarrow \mathbb {R}$
such that:
-
(i)
 $f_k(kp)=1$
and
$f_k(kp)=1$
and
 $f_k(q)=0$
for any
$f_k(q)=0$
for any
 $q\in k\Delta \cap \mathbb {Z}^n$
; and
$q\in k\Delta \cap \mathbb {Z}^n$
; and -
(ii) for any piecewise linear function
 $g_k$
satisfies the condition (i),
$g_k$
satisfies the condition (i), \begin{equation*}\int _{k\Delta }f_{p,k}(x)dV \geqslant \int _{k\Delta }g_k(x)dV.\end{equation*}
\begin{equation*}\int _{k\Delta }f_{p,k}(x)dV \geqslant \int _{k\Delta }g_k(x)dV.\end{equation*}
This is equivalent to defining hyperplanes
![]() $H_k:=\left \{L\left (\frac {x}{k}\right )=0\right \}$
with
$H_k:=\left \{L\left (\frac {x}{k}\right )=0\right \}$
with
![]() $L(p)\gt 0$
such that:
$L(p)\gt 0$
such that:
-
(i)
 $R_{p,k}^o:=\{L\left (\frac {x}{k}\right )\gt 0\}\cap k\Delta =\{kp\}$
; and
$R_{p,k}^o:=\{L\left (\frac {x}{k}\right )\gt 0\}\cap k\Delta =\{kp\}$
; and -
(ii) for any
 ${R_{p,k}^{\prime}}^o:=\{\hat {L}\left (\frac {x}{k}\right )\gt 0\}\cap k\Delta =\{kp\}$
,
${R_{p,k}^{\prime}}^o:=\{\hat {L}\left (\frac {x}{k}\right )\gt 0\}\cap k\Delta =\{kp\}$
, \begin{equation*}\textrm{Vol}(R_k^o)\geqslant \textrm{Vol}({R_k^{\prime}}^o).\end{equation*}
\begin{equation*}\textrm{Vol}(R_k^o)\geqslant \textrm{Vol}({R_k^{\prime}}^o).\end{equation*}
We denote
which is the base of the cone
![]() $\overline {R_{p,1}^o}$
. By the same argument as in the proof of Proposition 3.7, if there exists
$\overline {R_{p,1}^o}$
. By the same argument as in the proof of Proposition 3.7, if there exists
![]() $p$
such that
$p$
such that
![]() $\textrm{Vol}(Q_p)\geqslant d(d+1)$
, then
$\textrm{Vol}(Q_p)\geqslant d(d+1)$
, then
![]() $f_k$
do not satisfy the inequality (1) for all
$f_k$
do not satisfy the inequality (1) for all
![]() $k\gt \gt 0$
. The whole construction is called the cut a vertex technique as
$k\gt \gt 0$
. The whole construction is called the cut a vertex technique as
![]() $k\Delta =R_{p,k}^o \cap \{f_k=0\}$
, where we separate
$k\Delta =R_{p,k}^o \cap \{f_k=0\}$
, where we separate
![]() $k\Delta$
into a cone
$k\Delta$
into a cone
![]() $\overline {R_{p,k}}$
near the vertex
$\overline {R_{p,k}}$
near the vertex
![]() $kp$
and the remaining, and we can show that
$kp$
and the remaining, and we can show that
![]() $\Delta$
is not asymptotically Chow semistable by studying the properties of
$\Delta$
is not asymptotically Chow semistable by studying the properties of
![]() $\overline {R_{p,k}}$
or even only
$\overline {R_{p,k}}$
or even only
![]() $\overline {R_{p,1}}$
.
$\overline {R_{p,1}}$
.
Additionally, for
![]() $(\mathbb {P}^{n}, O(n+1))$
and
$(\mathbb {P}^{n}, O(n+1))$
and
![]() $((\mathbb {P}^1)^{n}, O(2,\ldots, 2))$
, under the above construction,
$((\mathbb {P}^1)^{n}, O(2,\ldots, 2))$
, under the above construction,
![]() $\overline {R_k^o}$
must be an
$\overline {R_k^o}$
must be an
![]() $n$
-dimensional simplex. Hence
$n$
-dimensional simplex. Hence
![]() $Q_p$
are
$Q_p$
are
![]() $(n-1)$
-dimensional simplices for all
$(n-1)$
-dimensional simplices for all
![]() $p$
, and the volume of
$p$
, and the volume of
![]() $Q_p$
is
$Q_p$
is
which is expected as we know that they are asymptotically Chow polystable.
In § 4, we will define a more restrictive type of polytopes, which are asymptotically Chow polystable.
4. Special polytopes
We first recall some definitions from toric geometry.
Definition 4.1. An integral polytope
![]() $P$
is reflexive if the boundary is given by the equations
$P$
is reflexive if the boundary is given by the equations
 \begin{equation*}\sum _{i=1}^n a_ix_i=\pm 1,\end{equation*}
\begin{equation*}\sum _{i=1}^n a_ix_i=\pm 1,\end{equation*}
where
![]() $a_i\in \mathbb {Z}$
. Or equivalently, there exists exactly one interior point
$a_i\in \mathbb {Z}$
. Or equivalently, there exists exactly one interior point
![]() $(0,\ldots, 0)$
.
$(0,\ldots, 0)$
.
Definition 4.2. An integral polytope
![]() $P$
is symmetric if there is exactly one fixed point of the symmetric group
$P$
is symmetric if there is exactly one fixed point of the symmetric group
![]() $G$
acting on
$G$
acting on
![]() $P$
.
$P$
.
Notice that if
![]() $P$
is reflexive, then the fixed point is
$P$
is reflexive, then the fixed point is
![]() $0$
, and the
$0$
, and the
![]() $G\lt SL(n, \mathbb {Z})$
action is given by the matrix multiplication. We now add one extra restriction on the symmetric reflexive polytopes.
$G\lt SL(n, \mathbb {Z})$
action is given by the matrix multiplication. We now add one extra restriction on the symmetric reflexive polytopes.
Definition 4.3. Let
![]() $P$
be an
$P$
be an
![]() $n$
-dimensional integral convex polytope on
$n$
-dimensional integral convex polytope on
![]() $\mathbb {R}^n$
. We say
$\mathbb {R}^n$
. We say
![]() $P$
has regular boundary if for any
$P$
has regular boundary if for any
![]() $k\in \mathbb {N}$
, there exists a triangulation of
$k\in \mathbb {N}$
, there exists a triangulation of
![]() $\partial kP$
which every ‘triangle’ is integrally isomorphic to
$\partial kP$
which every ‘triangle’ is integrally isomorphic to
the standard
![]() $(n-1)$
-dimensional simplex, (i.e. the intersection between different
$(n-1)$
-dimensional simplex, (i.e. the intersection between different
![]() $T_{n-1}^i$
are at the boundary) such that:
$T_{n-1}^i$
are at the boundary) such that:
-
(i) for any point
 $p\in \partial kP$
, the number of simplices intersecting with
$p\in \partial kP$
, the number of simplices intersecting with
 $p$
, denoted as
$p$
, denoted as
 $m_k(p)$
, is bounded by
$m_k(p)$
, is bounded by
 $n!$
(i.e.
$n!$
(i.e.
 $m_k(p)\leqslant n!$
); and
$m_k(p)\leqslant n!$
); and -
(ii) this is the sub-triangulation of each face.
Here, integrally isomorphic means one of the objects is obtained from another object by an integral rigid motion, i.e. the multiplication of a matrix
![]() $A\in SL(n, \mathbb {Z})$
and translation of
$A\in SL(n, \mathbb {Z})$
and translation of
![]() $v\in \mathbb {Z}^{n}$
.
$v\in \mathbb {Z}^{n}$
.
Remark 4.4. If two objects
![]() $P_1, P_2$
are integrally isomorphic, then for all
$P_1, P_2$
are integrally isomorphic, then for all
![]() $k$
,
$k$
,
![]() $kP_1$
has the same number of integral points as
$kP_1$
has the same number of integral points as
![]() $kP_2$
. Indeed, integral isomorphism is obtained by a bijection map
$kP_2$
. Indeed, integral isomorphism is obtained by a bijection map
![]() $\varphi \colon \mathbb {Z}^n\rightarrow \mathbb {Z}^n$
. So for each compact object
$\varphi \colon \mathbb {Z}^n\rightarrow \mathbb {Z}^n$
. So for each compact object
![]() $U\subset \mathbb {R}^n$
, the map
$U\subset \mathbb {R}^n$
, the map
![]() $\varphi \colon U\cap \mathbb {Z}^n\rightarrow \varphi (U\cap \mathbb {Z}^n)$
is a bijection.
$\varphi \colon U\cap \mathbb {Z}^n\rightarrow \varphi (U\cap \mathbb {Z}^n)$
is a bijection.
Definition 4.5. An integral convex polytope on
![]() $\mathbb {R}^n$
is called special if it is reflexive, weakly symmetric, and has a regular boundary. A Fano toric variety
$\mathbb {R}^n$
is called special if it is reflexive, weakly symmetric, and has a regular boundary. A Fano toric variety
![]() $(X,-K_X)$
is called special if the corresponding polytope is special.
$(X,-K_X)$
is called special if the corresponding polytope is special.
Example 4.6.
Suppose
![]() $P$
is a two-dimensional symmetric reflexive polytope, so then it is special. This is because the boundary of
$P$
is a two-dimensional symmetric reflexive polytope, so then it is special. This is because the boundary of
![]() $P$
is a loop, so every point must connect with two segments hence the boundary has a regular triangulation.
$P$
is a loop, so every point must connect with two segments hence the boundary has a regular triangulation.
Remark 4.7. The two-dimensional symmetric reflexive polytopes are
 \begin{align*} & X_3 :=\textrm{conv}\{(-1,-1), (1,0), (0,1)\}, X_4:=\textrm{conv}\{(\pm 1, 0), (0, \pm 1)\},\\&X_6:=\textrm{conv}\{(0,\pm 1), (\pm 1, 0), (1,-1), (-1,1)\}, X_8:=\textrm{conv}\{(\pm 1, \pm 1)\},\\&X_9:=\textrm{conv}\{(-1,-1), (2,-1), (-1, 2)\}\end{align*}
\begin{align*} & X_3 :=\textrm{conv}\{(-1,-1), (1,0), (0,1)\}, X_4:=\textrm{conv}\{(\pm 1, 0), (0, \pm 1)\},\\&X_6:=\textrm{conv}\{(0,\pm 1), (\pm 1, 0), (1,-1), (-1,1)\}, X_8:=\textrm{conv}\{(\pm 1, \pm 1)\},\\&X_9:=\textrm{conv}\{(-1,-1), (2,-1), (-1, 2)\}\end{align*}
Example 4.8.
The polytopes
![]() $D(X_3)$
,
$D(X_3)$
,
![]() $D(X_4)$
,
$D(X_4)$
,
![]() $D(X_6)$
,
$D(X_6)$
,
![]() $D(X_8)$
and
$D(X_8)$
and
![]() $ D(X_9)$
are symmetric and reflexive. However, among these five polytopes, only
$ D(X_9)$
are symmetric and reflexive. However, among these five polytopes, only
![]() $D(X_3)$
,
$D(X_3)$
,
![]() $D(X_4)$
and
$D(X_4)$
and
![]() $D(X_6)$
are special. For instance, the faces of
$D(X_6)$
are special. For instance, the faces of
![]() $D(X_8)$
are given by the triangles integrally isomorphic to
$D(X_8)$
are given by the triangles integrally isomorphic to
![]() $\textrm{conv}\{(-1,0),(1,0),(0,1)\}$
. As a result, for any
$\textrm{conv}\{(-1,0),(1,0),(0,1)\}$
. As a result, for any
![]() $k$
, and for the point
$k$
, and for the point
![]() $(0,0,\pm k)$
, there must be
$(0,0,\pm k)$
, there must be
![]() $2$
simplices attaching the vertex for each face. Therefore,
$2$
simplices attaching the vertex for each face. Therefore,
Similarly, we can see that for any triangulation for
![]() $D(X_9)$
,
$D(X_9)$
,
There are pictures indicating how to triangulate a face of
![]() $D(X_8)$
and a face of
$D(X_8)$
and a face of
![]() $D(X_9)$
in §
10
.
$D(X_9)$
in §
10
.
5. Properties of special polytopes
In this section, we study what results each assumption in the definition of the special toric varieties can provide, starting with reflexivity.
Lemma 5.1.
Let
![]() $P$
be a reflexive polytopes. Then, for all
$P$
be a reflexive polytopes. Then, for all
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
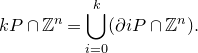 \begin{equation*}kP\cap \mathbb {Z}^n=\bigcup _{i=0}^k (\partial iP \cap \mathbb {Z}^n).\end{equation*}
\begin{equation*}kP\cap \mathbb {Z}^n=\bigcup _{i=0}^k (\partial iP \cap \mathbb {Z}^n).\end{equation*}
Proof.
Let
![]() $P$
be reflexive. Then
$P$
be reflexive. Then
![]() $(0,\ldots, 0)\in \partial (0P)$
by definition. Notice that, for any
$(0,\ldots, 0)\in \partial (0P)$
by definition. Notice that, for any
![]() $p=(p_1,\ldots, p_n)\neq 0 \in kP$
, there exists
$p=(p_1,\ldots, p_n)\neq 0 \in kP$
, there exists
![]() $\alpha$
and
$\alpha$
and
![]() $0\lt c_{\alpha }\lt k$
such that
$0\lt c_{\alpha }\lt k$
such that
But
![]() $p\in \mathbb {Z}^n$
implies
$p\in \mathbb {Z}^n$
implies
![]() $c_{\alpha \in \mathbb {Z}}$
, and hence
$c_{\alpha \in \mathbb {Z}}$
, and hence
![]() $p\in \partial c_{\alpha } P\cap \mathbb {Z}^n$
.
$p\in \partial c_{\alpha } P\cap \mathbb {Z}^n$
.
Also, we have the following.
Lemma 5.2.
Let
![]() $P$
be a reflexive
$P$
be a reflexive
![]() $n$
-dimensional polytope. Then
$n$
-dimensional polytope. Then
Proof.
Let
![]() $\bigcup _{i=1}^rQ_i=\partial P$
, where the
$\bigcup _{i=1}^rQ_i=\partial P$
, where the
![]() $Q_i$
are faces of
$Q_i$
are faces of
![]() $P$
. Then define
$P$
. Then define
Then
 \begin{equation*}P= \bigcup _{i=1}^r C(Q_i),\end{equation*}
\begin{equation*}P= \bigcup _{i=1}^r C(Q_i),\end{equation*}
and
 \begin{equation*}\textrm{Vol}(P)=\sum _{i=1}^r \textrm{Vol}(C(Q_i)).\end{equation*}
\begin{equation*}\textrm{Vol}(P)=\sum _{i=1}^r \textrm{Vol}(C(Q_i)).\end{equation*}
The assumption that
![]() $P$
is reflexive implies the height is 1 for any
$P$
is reflexive implies the height is 1 for any
![]() $C(Q_i)$
, so
$C(Q_i)$
, so
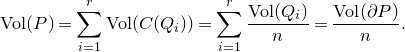 \begin{equation*}\textrm{Vol}(P)=\sum _{i=1}^r \textrm{Vol}(C(Q_i))=\sum _{i=1}^r \frac {\textrm{Vol}(Q_i)}{n}=\frac {\textrm{Vol}(\partial P)}{n}.\end{equation*}
\begin{equation*}\textrm{Vol}(P)=\sum _{i=1}^r \textrm{Vol}(C(Q_i))=\sum _{i=1}^r \frac {\textrm{Vol}(Q_i)}{n}=\frac {\textrm{Vol}(\partial P)}{n}.\end{equation*}
Lemma 5.3.
Suppose
![]() $f\colon P\rightarrow \mathbb {R}$
is a
$f\colon P\rightarrow \mathbb {R}$
is a
![]() $G$
-invariant convex function such that
$G$
-invariant convex function such that
Then
is convex, where
![]() $\sigma _{\partial P}\mid _x =d(l_{Q_i})\mid _x$
for
$\sigma _{\partial P}\mid _x =d(l_{Q_i})\mid _x$
for
![]() $x\in Q_i$
, the defining boundary function of the face
$x\in Q_i$
, the defining boundary function of the face
![]() $Q_i\subset \partial P$
.
$Q_i\subset \partial P$
.
Proof.
First, we have a map
![]() $\varphi \colon \partial P \times [0,1]\rightarrow P$
defined by
$\varphi \colon \partial P \times [0,1]\rightarrow P$
defined by
Notice that this map is surjective, that
![]() $\varphi (x,0)=0$
and that
$\varphi (x,0)=0$
and that
![]() $\varphi \mid _{\partial P\times (0,1]}$
is bijective. Hence any function
$\varphi \mid _{\partial P\times (0,1]}$
is bijective. Hence any function
![]() $f$
on
$f$
on
![]() $P$
can be represented by the function
$P$
can be represented by the function
Notice that
![]() $f(0)$
is the minimum, so
$f(0)$
is the minimum, so
![]() $f(x)\geqslant 0$
. We find that a (decreasing) sequence of smooth
$f(x)\geqslant 0$
. We find that a (decreasing) sequence of smooth
![]() $G$
-invariant convex functions
$G$
-invariant convex functions
![]() $f_i$
, with
$f_i$
, with
![]() $f_i(0)\geqslant 0$
, converges to
$f_i(0)\geqslant 0$
, converges to
![]() $f$
. Denote
$f$
. Denote
![]() $Q= \partial P$
. We define
$Q= \partial P$
. We define
![]() $g_i\colon Q\times [0,1]\rightarrow \mathbb {R}$
by
$g_i\colon Q\times [0,1]\rightarrow \mathbb {R}$
by
Now, by convexity, and since
![]() $f(0)$
is minimum,
$f(0)$
is minimum,
![]() $f$
is increasing along the segment
$f$
is increasing along the segment
![]() $\{(tx,t)\mid 0\leqslant t\leqslant 1\}$
, so it implies
$\{(tx,t)\mid 0\leqslant t\leqslant 1\}$
, so it implies
Also, convexity of
![]() $f_i$
implies
$f_i$
implies
As
we now compute the second derivative of
![]() $F_i$
. For
$F_i$
. For
![]() $n\geqslant 3$
, the second derivative of
$n\geqslant 3$
, the second derivative of
![]() $F_i$
is given by
$F_i$
is given by
 \begin{eqnarray*} \frac {d^2}{dt^2}\int _{tQ}f_i(x,t)d\sigma _Q &=&\frac {d^2}{dt^2}t^{n-1}\int _{Q}g_i(x,t)d\sigma _Q\\ &=&\frac {d}{dt}\left ((n-1)t^{n-2}\int _Qg_i\left (x,t\right )d\sigma _Q+t^{n-1}\int _Q\frac {dg_i}{dt}\left (x,t\right )d\sigma _Q\right )\\ &=&(n-1)(n-2)t^{n-3}\int _Qg_i\left (x,t\right )d\sigma _Q\\ &&+2(n-1)t^{n-2}\int _Q\frac {dg_i}{dt}\left (x,t\right )d\sigma _Q+t^{n-1}\int _Q \frac {d^2g_i}{dt^2}d\sigma _Q\\ &\geqslant & 0, \end{eqnarray*}
\begin{eqnarray*} \frac {d^2}{dt^2}\int _{tQ}f_i(x,t)d\sigma _Q &=&\frac {d^2}{dt^2}t^{n-1}\int _{Q}g_i(x,t)d\sigma _Q\\ &=&\frac {d}{dt}\left ((n-1)t^{n-2}\int _Qg_i\left (x,t\right )d\sigma _Q+t^{n-1}\int _Q\frac {dg_i}{dt}\left (x,t\right )d\sigma _Q\right )\\ &=&(n-1)(n-2)t^{n-3}\int _Qg_i\left (x,t\right )d\sigma _Q\\ &&+2(n-1)t^{n-2}\int _Q\frac {dg_i}{dt}\left (x,t\right )d\sigma _Q+t^{n-1}\int _Q \frac {d^2g_i}{dt^2}d\sigma _Q\\ &\geqslant & 0, \end{eqnarray*}
so all
![]() $F_i$
are convex. Thus
$F_i$
are convex. Thus
![]() $F$
is convex.
$F$
is convex.
Also, for
![]() $n=2$
,
$n=2$
,
Finally, for
![]() $n=1$
,
$n=1$
,
![]() $F(t)=f(-ta)+f(tb)$
for
$F(t)=f(-ta)+f(tb)$
for
![]() $P=[-a,b]$
, so
$P=[-a,b]$
, so
So
![]() $F_i^{\prime\prime}(t) \geqslant 0$
for all
$F_i^{\prime\prime}(t) \geqslant 0$
for all
![]() $i$
, which implies that
$i$
, which implies that
![]() $F(t)$
is convex.
$F(t)$
is convex.
As a remark, when we put
![]() $f(x)=c$
, then
$f(x)=c$
, then
![]() $F_c(t)= c\textrm{Vol}(\partial P)t^{n-1}$
, in which we can see that if
$F_c(t)= c\textrm{Vol}(\partial P)t^{n-1}$
, in which we can see that if
![]() $c\lt 0$
and
$c\lt 0$
and
![]() $n \geqslant 3$
,
$n \geqslant 3$
,
![]() $F_c$
is not convex on
$F_c$
is not convex on
![]() $[0,1]$
.
$[0,1]$
.
Corollary 5.4.
Suppose
![]() $P$
is symmetric. Then for all
$P$
is symmetric. Then for all
![]() $k\in \mathbb {R}$
, for all
$k\in \mathbb {R}$
, for all
![]() $G$
invariant convex functions
$G$
invariant convex functions
![]() $f\colon kP\rightarrow \mathbb {R}$
with
$f\colon kP\rightarrow \mathbb {R}$
with
![]() $\min _{x\in kP}f(x)=f(0)=0$
, we have
$\min _{x\in kP}f(x)=f(0)=0$
, we have
where
Also, equality holds if and only if
![]() $f=0$
.
$f=0$
.
Proof. Now
By Lemma 5.3,
![]() $F(t)$
is convex, and hence by the trapezoid rule, we have
$F(t)$
is convex, and hence by the trapezoid rule, we have
The final lemma is a property of a regular boundary.
Lemma 5.5.
Let
![]() $P$
have a regular boundary. Then for any
$P$
have a regular boundary. Then for any
![]() $k$
, and for any convex function
$k$
, and for any convex function
![]() $f$
, we have
$f$
, we have
Proof.
Let
![]() $n$
be the dimension of
$n$
be the dimension of
![]() $P$
. Then its boundary can be triangulated by the
$P$
. Then its boundary can be triangulated by the
![]() $(n-1)$
simplex
$(n-1)$
simplex
![]() $T_{n-1}$
. Let the vertex point of
$T_{n-1}$
. Let the vertex point of
![]() $T_{n-1}^{\alpha }$
be
$T_{n-1}^{\alpha }$
be
![]() $p_0^{\alpha },\ldots, p_{n-1}^{\alpha }$
, so then convexity implies all simplex
$p_0^{\alpha },\ldots, p_{n-1}^{\alpha }$
, so then convexity implies all simplex
![]() $T_{n-1}$
have the property
$T_{n-1}$
have the property
 \begin{equation*}\int _{T_{n-1}}f(x)d\sigma \leqslant \textrm{Vol}(T_{n-1})\sum _{i=0}^{n-1}\frac {f(p_i)}{n}=\sum _{i=0}^{n-1}\frac {f(p_i)}{n!}. \end{equation*}
\begin{equation*}\int _{T_{n-1}}f(x)d\sigma \leqslant \textrm{Vol}(T_{n-1})\sum _{i=0}^{n-1}\frac {f(p_i)}{n}=\sum _{i=0}^{n-1}\frac {f(p_i)}{n!}. \end{equation*}
Therefore, if we denote
![]() $n(p)$
to be the number of simplex touching the point
$n(p)$
to be the number of simplex touching the point
![]() $p$
, then the regular boundary assumption means
$p$
, then the regular boundary assumption means
![]() $n(p) \leqslant n!$
, which implies
$n(p) \leqslant n!$
, which implies
 \begin{align*} \int _{\partial kP}f(x)d\sigma =&\sum _{\alpha } \int _{T_{n-1}^{\alpha }}f(x)d\sigma \leqslant \sum _{\alpha }\sum _{i=0}^{n-1}\dfrac {f(p_i^{\alpha })}{n!} \displaystyle =\sum _{p\in \partial kP \cap \mathbb {Z}^n}\frac { n(p)f(p)}{n!}\\ \leqslant &\sum _{p\in \partial kP \cap \mathbb {Z}^n} \frac { n!f(p)}{n!} =\sum _{p\in \partial kP \cap \mathbb {Z}^n} f(p). \end{align*}
\begin{align*} \int _{\partial kP}f(x)d\sigma =&\sum _{\alpha } \int _{T_{n-1}^{\alpha }}f(x)d\sigma \leqslant \sum _{\alpha }\sum _{i=0}^{n-1}\dfrac {f(p_i^{\alpha })}{n!} \displaystyle =\sum _{p\in \partial kP \cap \mathbb {Z}^n}\frac { n(p)f(p)}{n!}\\ \leqslant &\sum _{p\in \partial kP \cap \mathbb {Z}^n} \frac { n!f(p)}{n!} =\sum _{p\in \partial kP \cap \mathbb {Z}^n} f(p). \end{align*}
6. Chow stabilities of special polytopes
We now show that a special polytope is asymptotically Chow polystable.
Theorem 6.1.
Let
![]() $P$
be a special polytope. Then
$P$
be a special polytope. Then
![]() $P$
is asymptotically Chow polystable.
$P$
is asymptotically Chow polystable.
Proof.
First, denote
![]() $\chi (kP):=\#\{kP\cap \mathbb {Z}^n\}$
, so then
$\chi (kP):=\#\{kP\cap \mathbb {Z}^n\}$
, so then
 \begin{equation*}\frac {1}{\textrm{Vol}(kP)}\int _{kP}c\, dV=\frac {1}{\chi (kP)}\sum _{p\in kP\cap \mathbb {Z}^n}c. \end{equation*}
\begin{equation*}\frac {1}{\textrm{Vol}(kP)}\int _{kP}c\, dV=\frac {1}{\chi (kP)}\sum _{p\in kP\cap \mathbb {Z}^n}c. \end{equation*}
Second,
![]() $P$
is reflexive and symmetric implies that for any
$P$
is reflexive and symmetric implies that for any
![]() $G$
invariant convex function
$G$
invariant convex function
![]() $f$
,
$f$
,
Therefore, to show that the inequality (1) holds for any
![]() $G$
-invariant convex function
$G$
-invariant convex function
![]() $f$
, we only need to show that the inequality (1) holds for all
$f$
, we only need to show that the inequality (1) holds for all
![]() $G$
-invariant convex functions
$G$
-invariant convex functions
![]() $f$
satisfying
$f$
satisfying
.
Let
![]() $f$
be a
$f$
be a
![]() $G$
-invariant convex function satisfying
$G$
-invariant convex function satisfying
By Corollary 5.4,
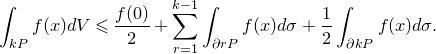 \begin{equation*}\int _{kP} f(x)dV\leqslant \frac {f(0)}{2}+ \sum _{r=1}^{k-1}\int _{\partial rP} f(x)d\sigma +\frac {1}{2}\int _{\partial kP} f(x)d\sigma . \end{equation*}
\begin{equation*}\int _{kP} f(x)dV\leqslant \frac {f(0)}{2}+ \sum _{r=1}^{k-1}\int _{\partial rP} f(x)d\sigma +\frac {1}{2}\int _{\partial kP} f(x)d\sigma . \end{equation*}
Lemma 5.5 implies
 \begin{align*}\int _{kP} f(x)dV & \leqslant \frac {f(0)}{2}+ \sum _{r=1}^{k-1}\sum _{\partial rP \cap \mathbb {Z}^{n}} f(p)+\frac {1}{2}\sum _{\partial kP\cap \mathbb {Z}^n} f(p)\\ &=\sum _{r=0}^k \sum _{p\in \partial rP\cap \mathbb {Z}^n}f(p)- \frac {f(0)}{2}- \frac {1}{2}\sum _{p\in \partial kP\cap \mathbb {Z}^n}f(p). \end{align*}
\begin{align*}\int _{kP} f(x)dV & \leqslant \frac {f(0)}{2}+ \sum _{r=1}^{k-1}\sum _{\partial rP \cap \mathbb {Z}^{n}} f(p)+\frac {1}{2}\sum _{\partial kP\cap \mathbb {Z}^n} f(p)\\ &=\sum _{r=0}^k \sum _{p\in \partial rP\cap \mathbb {Z}^n}f(p)- \frac {f(0)}{2}- \frac {1}{2}\sum _{p\in \partial kP\cap \mathbb {Z}^n}f(p). \end{align*}
Therefore, Lemma 5.1 implies
 \begin{equation*}\int _{kP} f(x)dV\leqslant \sum _{kP \cap \mathbb {Z}^{n}} f(p)- \frac {1}{2}f(0)-\frac {1}{2} \sum _{p\in \partial kP\cap \mathbb {Z}^n}f(p). \end{equation*}
\begin{equation*}\int _{kP} f(x)dV\leqslant \sum _{kP \cap \mathbb {Z}^{n}} f(p)- \frac {1}{2}f(0)-\frac {1}{2} \sum _{p\in \partial kP\cap \mathbb {Z}^n}f(p). \end{equation*}
Therefore,
 \begin{align*} \frac {1}{\textrm{Vol}(kP)}\int _{kP} f(x)dV =& \frac {1}{\chi (kP)}\int _{kP} f(x)dV +\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV\\ &\leqslant \frac {1}{\chi (kP)}\left ( \sum _{r=0}^{k}\int _{\partial rP} f(x)d\sigma -\frac {1}{2}f(0)-\frac {1}{2}\sum _{p\in \partial kP\cap \mathbb {Z}^n } f(p)\right )\\ &+\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV\\ &\leqslant \frac {1}{\chi (kP)} \sum _{r=0}^k \sum _{p\in \partial rP}f(p)- \frac {1}{2 \chi (kP)}\left ( f(0)+\sum _{p\in \partial kP\cap \mathbb {Z}^n} f(p)\right )\\ &+\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV \qquad (\text {Lemma 5.5})\\ &= \frac {1}{\chi (kP)} \sum _{p\in kP}f(p)- \frac {1}{2 \chi (kP)}\left ( f(0)+\sum _{p\in \partial kP\cap \mathbb {Z}^n} f(p)\right )\\ &+\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV \qquad (\text {Lemma 5.1}). \end{align*}
\begin{align*} \frac {1}{\textrm{Vol}(kP)}\int _{kP} f(x)dV =& \frac {1}{\chi (kP)}\int _{kP} f(x)dV +\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV\\ &\leqslant \frac {1}{\chi (kP)}\left ( \sum _{r=0}^{k}\int _{\partial rP} f(x)d\sigma -\frac {1}{2}f(0)-\frac {1}{2}\sum _{p\in \partial kP\cap \mathbb {Z}^n } f(p)\right )\\ &+\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV\\ &\leqslant \frac {1}{\chi (kP)} \sum _{r=0}^k \sum _{p\in \partial rP}f(p)- \frac {1}{2 \chi (kP)}\left ( f(0)+\sum _{p\in \partial kP\cap \mathbb {Z}^n} f(p)\right )\\ &+\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV \qquad (\text {Lemma 5.5})\\ &= \frac {1}{\chi (kP)} \sum _{p\in kP}f(p)- \frac {1}{2 \chi (kP)}\left ( f(0)+\sum _{p\in \partial kP\cap \mathbb {Z}^n} f(p)\right )\\ &+\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV \qquad (\text {Lemma 5.1}). \end{align*}
So we only need to show
 \begin{equation*}- \frac {1}{2 \chi (kP)}\left ( f(0)+\sum _{p\in \partial kP\cap \mathbb {Z}^n} f(p)\right )+\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV \leqslant 0.\end{equation*}
\begin{equation*}- \frac {1}{2 \chi (kP)}\left ( f(0)+\sum _{p\in \partial kP\cap \mathbb {Z}^n} f(p)\right )+\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV \leqslant 0.\end{equation*}
That is,
 \begin{align}\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV\leqslant \frac {1}{2 \chi (kP)}\left ( f(0)+\sum _{p\in \partial kP\cap \mathbb {Z}^n} f(p)\right ). \end{align}
\begin{align}\left (\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\right )\int _{kP} f(x)dV\leqslant \frac {1}{2 \chi (kP)}\left ( f(0)+\sum _{p\in \partial kP\cap \mathbb {Z}^n} f(p)\right ). \end{align}
Now, we can triangulate
![]() $kP$
by
$kP$
by
![]() $C_{\alpha }:=\textrm{conv} \{(0,\ldots, 0),T_{n-1}^{\alpha }\}$
, where
$C_{\alpha }:=\textrm{conv} \{(0,\ldots, 0),T_{n-1}^{\alpha }\}$
, where
![]() $\bigcup _{\alpha }T_{n-1}^{\alpha }$
is the regular triangulation on
$\bigcup _{\alpha }T_{n-1}^{\alpha }$
is the regular triangulation on
![]() $\partial kP$
,
$\partial kP$
,
![]() $\textrm{Vol}(C_{\alpha })=\frac {k}{n(n-1)!}=\frac {k}{n!}$
, and by convexity,
$\textrm{Vol}(C_{\alpha })=\frac {k}{n(n-1)!}=\frac {k}{n!}$
, and by convexity,
 \begin{align*} \int _{kP} f(x)dV \leqslant & \sum _{\alpha } \textrm{Vol}(C_{\alpha })\sum _i \frac {f(0)+f(p_0^{\alpha })+\cdots +f(p_{n-1}^{\alpha })}{n+1}\\ =&\sum _{p\in \partial kP}\frac {k n(p) f(p)}{(n!) (n+1)}+ \frac {\textrm{Vol}(\partial kP)}{\textrm{Vol}(C_{n-1})} \frac {k}{n! (n+1)}f(0)\\ \leqslant & \sum _{p\in \partial kP} \frac {kf(p)}{n+1}+ \textrm{Vol}(\partial kP) \frac {k}{n(n+1)}f(0). \end{align*}
\begin{align*} \int _{kP} f(x)dV \leqslant & \sum _{\alpha } \textrm{Vol}(C_{\alpha })\sum _i \frac {f(0)+f(p_0^{\alpha })+\cdots +f(p_{n-1}^{\alpha })}{n+1}\\ =&\sum _{p\in \partial kP}\frac {k n(p) f(p)}{(n!) (n+1)}+ \frac {\textrm{Vol}(\partial kP)}{\textrm{Vol}(C_{n-1})} \frac {k}{n! (n+1)}f(0)\\ \leqslant & \sum _{p\in \partial kP} \frac {kf(p)}{n+1}+ \textrm{Vol}(\partial kP) \frac {k}{n(n+1)}f(0). \end{align*}
Therefore, in order to show equation (2), it suffices to show that we have
 \begin{equation*} \left (\!\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\!\right )\!\left (\sum _{p\in \partial kP} \frac {kf(p)}{n+1}+ \textrm{Vol}(\partial kP) \frac {k}{(n+1)n}f(0)\!\right )\!\leqslant \frac {1}{2 \chi (kP)}\!\left (\! f(0)+\sum _{p\in \partial kP\cap \mathbb {Z}^n}\! f(p)\!\right )\!,\end{equation*}
\begin{equation*} \left (\!\frac {1}{\textrm{Vol}(kP)}-\frac {1}{\chi (kP)}\!\right )\!\left (\sum _{p\in \partial kP} \frac {kf(p)}{n+1}+ \textrm{Vol}(\partial kP) \frac {k}{(n+1)n}f(0)\!\right )\!\leqslant \frac {1}{2 \chi (kP)}\!\left (\! f(0)+\sum _{p\in \partial kP\cap \mathbb {Z}^n}\! f(p)\!\right )\!,\end{equation*}
or
 \begin{align*} \left [\left (\frac {\chi (kP)-\textrm{Vol}(kP)}{\textrm{Vol}(kP)}\right )\right.& \left.\left (\frac {k }{n(n+1)}{\textrm{Vol}(\partial kP)}\right )-\left (\frac {1}{2}\right )\right ]f(0)\\ \leqslant & \left (\frac {1}{2}-\left (\frac {k}{n+1}\right )\left (\frac {\chi (kP)-\textrm{Vol}(kP)}{\textrm{Vol}(kP)}\right )\right )\sum _{p\in \partial kP} f(p). \end{align*}
\begin{align*} \left [\left (\frac {\chi (kP)-\textrm{Vol}(kP)}{\textrm{Vol}(kP)}\right )\right.& \left.\left (\frac {k }{n(n+1)}{\textrm{Vol}(\partial kP)}\right )-\left (\frac {1}{2}\right )\right ]f(0)\\ \leqslant & \left (\frac {1}{2}-\left (\frac {k}{n+1}\right )\left (\frac {\chi (kP)-\textrm{Vol}(kP)}{\textrm{Vol}(kP)}\right )\right )\sum _{p\in \partial kP} f(p). \end{align*}
By assumption,
![]() $f(0)=\min _{p\in kP}f(p)=0$
, so we only need to show
$f(0)=\min _{p\in kP}f(p)=0$
, so we only need to show
By Lemma 3.6,
![]() $\chi (kP)=\textrm{Vol}(P)k^n+\frac {1}{2}\textrm{Vol}(\partial P)k^{n-1}+r(k)$
, where
$\chi (kP)=\textrm{Vol}(P)k^n+\frac {1}{2}\textrm{Vol}(\partial P)k^{n-1}+r(k)$
, where
![]() $r(k)= a_{n-2}k^{n-2}+ \cdots +a_1 k+1$
is a polynomial, and
$r(k)= a_{n-2}k^{n-2}+ \cdots +a_1 k+1$
is a polynomial, and
![]() $a_i$
depends on
$a_i$
depends on
![]() $P$
only, so
$P$
only, so
Using Lemma 5.2,
 \begin{align*} \left (\frac {k}{n+1}\right )\left (\frac {\chi (kP)-\textrm{Vol}(kP)}{\textrm{Vol}(kP)}\right ) = &\frac {k}{n+1}\left (\frac {\textrm{Vol}(\partial P)}{k \textrm{Vol}(P)}+r(k)\frac {k^{-n}}{\textrm{Vol}(P)}\right )\\ =&\frac {k}{n+1}\left (\frac {n}{k}+r(k)\frac {k^{1-n}}{\textrm{Vol}(P)}\right )\\ =&\frac {n}{2(n+1)}+r(k)\frac {k^{1-n}}{\textrm{Vol}(P)}. \end{align*}
\begin{align*} \left (\frac {k}{n+1}\right )\left (\frac {\chi (kP)-\textrm{Vol}(kP)}{\textrm{Vol}(kP)}\right ) = &\frac {k}{n+1}\left (\frac {\textrm{Vol}(\partial P)}{k \textrm{Vol}(P)}+r(k)\frac {k^{-n}}{\textrm{Vol}(P)}\right )\\ =&\frac {k}{n+1}\left (\frac {n}{k}+r(k)\frac {k^{1-n}}{\textrm{Vol}(P)}\right )\\ =&\frac {n}{2(n+1)}+r(k)\frac {k^{1-n}}{\textrm{Vol}(P)}. \end{align*}
Therefore, there exists
![]() $C$
such that
$C$
such that
for all
![]() $k\geqslant C$
, and hence
$k\geqslant C$
, and hence
which shows our theorem.
Example 6.2 (See also [Reference Lee, Li, Sturm and WangLLSW19]). By Example 4.6 and Remark 4.7
, all two-dimensional symmetric reflexive polytopes are special, which are
![]() $X_i$
for
$X_i$
for
![]() $i=3,4,6,8,9$
, and hence the above varieties are asymptotically Chow polystable.
$i=3,4,6,8,9$
, and hence the above varieties are asymptotically Chow polystable.
7. Regular triangulation of an
 $n$
simplex
$n$
simplex
To find higher-dimensional examples, we first need to know how to triangulate a polytope in higher dimensions. In general, it may be very difficult, but at least we can triangulate a polytope
![]() $kP$
by the following.
$kP$
by the following.
-
(i) Triangulate
 $P$
into simplices.
$P$
into simplices. -
(ii) Triangulate
 $kP$
, by first enlarging the triangulation on
$kP$
, by first enlarging the triangulation on
 $P$
, then triangulating
$P$
, then triangulating
 $kP$
by enlarged simplices
$kP$
by enlarged simplices
 $kT_n$
. After that, further triangulate every enlarged
$kT_n$
. After that, further triangulate every enlarged
 $n$
simplex
$n$
simplex
 $kT_n$
into simplices.
$kT_n$
into simplices.
So we need to know how to triangulate a simplex
![]() $kT_n:= \textrm{conv}\{(0,\ldots, 0), ke_i\mid i=1,\ldots, n\}$
, where
$kT_n:= \textrm{conv}\{(0,\ldots, 0), ke_i\mid i=1,\ldots, n\}$
, where
![]() $ke_1=(k,0,\ldots, 0), \ldots, ke_n=(0,\ldots, 0,k)$
. As a remark, the Lemma 7.1 is also proven in [Reference Lee and YotsutaniLY24], but for completeness, we will provide the proof here as well.
$ke_1=(k,0,\ldots, 0), \ldots, ke_n=(0,\ldots, 0,k)$
. As a remark, the Lemma 7.1 is also proven in [Reference Lee and YotsutaniLY24], but for completeness, we will provide the proof here as well.
Lemma 7.1 (Lemma A1 in [Reference Lee and YotsutaniLY24]). For any
![]() $p\in \mathbb {Z}^n$
, there exists a simplex triangulation
$p\in \mathbb {Z}^n$
, there exists a simplex triangulation
![]() $T$
of
$T$
of
![]() $\mathbb {R}^n$
such that
$\mathbb {R}^n$
such that
![]() $n(p)=(n+1)!$
. Moreover, this triangulation
$n(p)=(n+1)!$
. Moreover, this triangulation
![]() $T$
can triangulate the simplex
$T$
can triangulate the simplex
so that
for all
![]() $p\in ((n-k)\text {-faces of }k\Delta _n)^o\cap \mathbb {Z}^n$
.
$p\in ((n-k)\text {-faces of }k\Delta _n)^o\cap \mathbb {Z}^n$
.
Proof.
We modify an idea from [Reference HatcherHat02, p. 112] for the construction. Let
![]() $I=[0,1]$
be the unit interval in
$I=[0,1]$
be the unit interval in
![]() $\mathbb {R}$
. After taking an appropriate parallel transformation, we pick up one vertex
$\mathbb {R}$
. After taking an appropriate parallel transformation, we pick up one vertex
![]() $p$
from
$p$
from
![]() $\mathcal V(I^n)$
.
$\mathcal V(I^n)$
.
First, we triangulate the
![]() $n$
-dimensional cube
$n$
-dimensional cube
![]() $I^n$
into exactly
$I^n$
into exactly
![]() $n!$
copies of an
$n!$
copies of an
![]() $n$
-simplex
$n$
-simplex
![]() $\Delta _n$
. For the vertex
$\Delta _n$
. For the vertex
![]() $p\in \mathcal V(I^n)$
, we construct such a triangulation by induction on
$p\in \mathcal V(I^n)$
, we construct such a triangulation by induction on
![]() $n$
. Since the vertex
$n$
. Since the vertex
![]() $p$
has
$p$
has
![]() $n$
hyperfaces
$n$
hyperfaces
![]() $F_1, \dots, F_n \subset \Delta _n$
opposite it, we regard each
$F_1, \dots, F_n \subset \Delta _n$
opposite it, we regard each
![]() $F_i$
as an
$F_i$
as an
![]() $(n-1)$
-cube. By the assumption of inductive argument on
$(n-1)$
-cube. By the assumption of inductive argument on
![]() $n$
, each
$n$
, each
![]() $F_i$
can be triangulated into
$F_i$
can be triangulated into
![]() $(n-1)!$
copies of an
$(n-1)!$
copies of an
![]() $(n-1)$
-simplex such as
$(n-1)$
-simplex such as
 \begin{equation*} F_i=\bigcup _{j=1}^{(n-1)!}\Delta _{n-1}^{(j)}. \end{equation*}
\begin{equation*} F_i=\bigcup _{j=1}^{(n-1)!}\Delta _{n-1}^{(j)}. \end{equation*}
Let
![]() $\mathcal {V}(\Delta _{n-1}^{(j)})=\{q_1^{(j)}, \dots, q_n^{(j)}\}$
. Then,
$\mathcal {V}(\Delta _{n-1}^{(j)})=\{q_1^{(j)}, \dots, q_n^{(j)}\}$
. Then,
![]() $\mathrm {conv}\{p, q_1^{(j)}, \dots, q_n^{(j)}\}$
gives an
$\mathrm {conv}\{p, q_1^{(j)}, \dots, q_n^{(j)}\}$
gives an
![]() $n$
-simplex for each
$n$
-simplex for each
![]() $j$
, and hence we have
$j$
, and hence we have
![]() $n\times (n-1)!=n!$
copies of an
$n\times (n-1)!=n!$
copies of an
![]() $n$
-simplex by considering all
$n$
-simplex by considering all
![]() $n$
hyperfaces
$n$
hyperfaces
![]() $F_1, \dots, F_n$
.
$F_1, \dots, F_n$
.
Second, we denote by
![]() $T(I^n)$
this triangulation of
$T(I^n)$
this triangulation of
![]() $I^n$
into exactly
$I^n$
into exactly
![]() $n!$
simplices. Then we use parallel transformations of
$n!$
simplices. Then we use parallel transformations of
![]() $T(I^n)$
for obtaining a triangulation of
$T(I^n)$
for obtaining a triangulation of
![]() $\mathbb {R}^n$
such that
$\mathbb {R}^n$
such that
![]() $n(p)=(n+1)!$
.
$n(p)=(n+1)!$
.
For
![]() $n=1$
, this is obvious. For
$n=1$
, this is obvious. For
![]() $n=2$
,
$n=2$
,
![]() $T(I^2)$
consists of two triangles (see Figure 1). Keeping this and taking parallel transformations of
$T(I^2)$
consists of two triangles (see Figure 1). Keeping this and taking parallel transformations of
![]() $T(I^2)$
around the vertex
$T(I^2)$
around the vertex
![]() $p$
, we obtain the triangulation of
$p$
, we obtain the triangulation of
![]() $\mathbb {R}^2$
with
$\mathbb {R}^2$
with
![]() $n(p)=3!$
. See Figure 2, also the Figure 3 for the parallel transformation in finite steps.
$n(p)=3!$
. See Figure 2, also the Figure 3 for the parallel transformation in finite steps.
For arbitrary
![]() $n\in \mathbb {N}$
, let us denote the set of
$n\in \mathbb {N}$
, let us denote the set of
![]() $2^n$
vertices of the
$2^n$
vertices of the
![]() $n$
-cube by
$n$
-cube by
Then we see that
![]() $n(p)$
is given by the number of all simplices in
$n(p)$
is given by the number of all simplices in
![]() $T(I^n)$
whose vertices lie in
$T(I^n)$
whose vertices lie in
![]() $\mathcal V(I^n)$
. If we denote by
$\mathcal V(I^n)$
. If we denote by
![]() $T(\mathbb {R}^n)$
the triangulation of
$T(\mathbb {R}^n)$
the triangulation of
![]() $\mathbb {R}^n$
induced by
$\mathbb {R}^n$
induced by
![]() $T(I^n)$
, we see that
$T(I^n)$
, we see that
![]() $n(p)$
coincides with the value of the characteristic function
$n(p)$
coincides with the value of the characteristic function
![]() $\varphi _{T(I^n)}\colon \mathbb {Z}^n \rightarrow \mathbb {R}$
defined by
$\varphi _{T(I^n)}\colon \mathbb {Z}^n \rightarrow \mathbb {R}$
defined by
where the summation is over all
![]() $n$
-simplices of
$n$
-simplices of
![]() $T(\mathbb {R}^n)$
for which
$T(\mathbb {R}^n)$
for which
![]() $p$
is a vertex (see, [Reference Gelfand, Kapranov and ZelevinskyGKZ94, p. 220]). Consequently, we have
$p$
is a vertex (see, [Reference Gelfand, Kapranov and ZelevinskyGKZ94, p. 220]). Consequently, we have
![]() $n(p)=(n+1)!$
, which proves the first part.
$n(p)=(n+1)!$
, which proves the first part.

Figure 1. Triangulation of
![]() $I^2$
.
$I^2$
.

Figure 2. Triangulation of
![]() $\mathbb {R}^2$
induced from
$\mathbb {R}^2$
induced from
![]() $I^2$
.
$I^2$
.

Figure 3. Triangulation of a 2-simplex and rectangle.
For the second part, by taking a suitable
![]() $k\Delta _n\subset \mathbb {R}^n$
, the triangulation of
$k\Delta _n\subset \mathbb {R}^n$
, the triangulation of
![]() $\mathbb {R}^n$
induced a triangulation of
$\mathbb {R}^n$
induced a triangulation of
![]() $k\Delta _n$
(see the red triangle in Figure 2). Moreover, an action of the permutation group
$k\Delta _n$
(see the red triangle in Figure 2). Moreover, an action of the permutation group
![]() $\mathcal {S}_{n+1}$
on
$\mathcal {S}_{n+1}$
on
![]() $k\Delta _n$
(which permute the vertices) induces the action on the triangulation
$k\Delta _n$
(which permute the vertices) induces the action on the triangulation
![]() $T$
in
$T$
in
![]() $k\Delta _n$
. Consequently, the stabilizer group of
$k\Delta _n$
. Consequently, the stabilizer group of
![]() $p$
in
$p$
in
![]() $\mathcal {S}_{n+1}$
is
$\mathcal {S}_{n+1}$
is
![]() $\mathcal {S}_{k+1}$
, which implies that
$\mathcal {S}_{k+1}$
, which implies that
for
![]() $p \in ((n-k)\text {-faces of } k\Delta _n)^o\cap \mathbb {Z}^n$
.
$p \in ((n-k)\text {-faces of } k\Delta _n)^o\cap \mathbb {Z}^n$
.
8. Another sufficient condition of Chow stabilities on reflexive toric varieties
Theorem 8.1.
Let
![]() $P$
be a reflexive polytope such that all the Futaki–Ono invariants vanish, and one has a triangulation on
$P$
be a reflexive polytope such that all the Futaki–Ono invariants vanish, and one has a triangulation on
![]() $kP$
by
$kP$
by
![]() $n$
simplices, and a triangulation on
$n$
simplices, and a triangulation on
![]() $\partial kP$
by
$\partial kP$
by
![]() $(n-1)$
simplices, We let
$(n-1)$
simplices, We let
![]() $n(p;k)$
be the number of
$n(p;k)$
be the number of
![]() $n$
simplices attached to
$n$
simplices attached to
![]() $p\in kP$
in the first triangulation, and
$p\in kP$
in the first triangulation, and
![]() $m(p;k)$
be the number of
$m(p;k)$
be the number of
![]() $(n-1)$
simplices attached to
$(n-1)$
simplices attached to
![]() $p\in \partial kP$
in the second. Suppose
$p\in \partial kP$
in the second. Suppose
![]() $n(p;k)\leqslant (n+1)!$
for all
$n(p;k)\leqslant (n+1)!$
for all
![]() $p\neq 0$
and
$p\neq 0$
and
for all
![]() $k\gt \gt 0$
and for all
$k\gt \gt 0$
and for all
![]() $p\in \partial kP$
. Then
$p\in \partial kP$
. Then
![]() $P$
is asymptotically Chow polystable.
$P$
is asymptotically Chow polystable.
Proof.
First,
![]() $P$
is weakly symmetric implies that we can assume
$P$
is weakly symmetric implies that we can assume
![]() $f(0)=\textrm{min}_{x\in P}f(x)\geqslant 0$
. Now,
$f(0)=\textrm{min}_{x\in P}f(x)\geqslant 0$
. Now,
Notice that
 \begin{equation*}\int _{kP} f(x)dV \leqslant \sum _{p\in kP}\frac {n(p;k)f(p)}{(n+1)!}\leqslant \sum _{p\in kP}f(p)-\sum _{p\in \partial kP}\frac {(n+1)!-n(p;k)}{(n+1)!}f(p).\end{equation*}
\begin{equation*}\int _{kP} f(x)dV \leqslant \sum _{p\in kP}\frac {n(p;k)f(p)}{(n+1)!}\leqslant \sum _{p\in kP}f(p)-\sum _{p\in \partial kP}\frac {(n+1)!-n(p;k)}{(n+1)!}f(p).\end{equation*}
Also, as in the proof of theorem 6.1, using the triangulation of
![]() $\partial kP$
, we triangulate
$\partial kP$
, we triangulate
![]() $kP$
such that each component is the convex hull of the origin and the simplex on
$kP$
such that each component is the convex hull of the origin and the simplex on
![]() $\partial (kP)$
, so we have
$\partial (kP)$
, so we have
 \begin{equation*}\int _{kP} f(p)\, dV \leqslant \sum _{p\in \partial kP}\frac {m(p;k)kf(p)}{(n)!(n+1)}+\textrm{Vol}(kP)\frac {f(0)}{(n+1)}.\end{equation*}
\begin{equation*}\int _{kP} f(p)\, dV \leqslant \sum _{p\in \partial kP}\frac {m(p;k)kf(p)}{(n)!(n+1)}+\textrm{Vol}(kP)\frac {f(0)}{(n+1)}.\end{equation*}
Also,
By assumption, we may assume
![]() $f(0)=0$
is the minimum, and therefore
$f(0)=0$
is the minimum, and therefore
 \begin{align*} &\frac {1}{\textrm{Vol}(kP)}\int _{kP} f(x)\, dV\\ &\leqslant \frac {1}{\chi (kP)} \left (\sum _{p\in kP}f(p)-\sum _{p\in \partial kP}\frac {(n+1)!-n(p;k)}{(n+1)!}f(p)\right )\\ &\quad + \left (\frac {nk^{-1}}{2\chi (kP)}+\frac {O(k^{-2})}{\chi (kP)}\right )\left (\sum _{p\in \partial kP}\frac {m(p;k)kf(p)}{(n)!(n+1)}+\textrm{Vol}(kP)\frac {f(0)}{(n+1)}\right )\\ &= \frac {1}{\chi (kP)}\sum _{p\in kP}f(p) +\frac {1}{(n+1)!\chi (kP)} \left (\left (\frac {n}{2}+O(k^{-1})\right )m(p;k)- ((n+1)!-n(p;k))\right ) \sum _{p\in \partial kP}f(p). \end{align*}
\begin{align*} &\frac {1}{\textrm{Vol}(kP)}\int _{kP} f(x)\, dV\\ &\leqslant \frac {1}{\chi (kP)} \left (\sum _{p\in kP}f(p)-\sum _{p\in \partial kP}\frac {(n+1)!-n(p;k)}{(n+1)!}f(p)\right )\\ &\quad + \left (\frac {nk^{-1}}{2\chi (kP)}+\frac {O(k^{-2})}{\chi (kP)}\right )\left (\sum _{p\in \partial kP}\frac {m(p;k)kf(p)}{(n)!(n+1)}+\textrm{Vol}(kP)\frac {f(0)}{(n+1)}\right )\\ &= \frac {1}{\chi (kP)}\sum _{p\in kP}f(p) +\frac {1}{(n+1)!\chi (kP)} \left (\left (\frac {n}{2}+O(k^{-1})\right )m(p;k)- ((n+1)!-n(p;k))\right ) \sum _{p\in \partial kP}f(p). \end{align*}
Therefore, if
then the inequality holds. Therefore, if for all
![]() $k$
, for all
$k$
, for all
![]() $p\in \partial kP$
,
$p\in \partial kP$
,
then
![]() $P$
is asymptotically Chow polystable.
$P$
is asymptotically Chow polystable.
Remark 8.2. We cannot generalize this statement from a reflexive polytope to an integral polytope as the inequalities
 \begin{equation*}\int _{kP} f(p)\, dV \leqslant \sum _{p\in \partial kP}\frac {m(p;k)kf(p)}{(n)!(n+1)}+\textrm{Vol}(kP)\frac {f(0)}{(n+1)} \end{equation*}
\begin{equation*}\int _{kP} f(p)\, dV \leqslant \sum _{p\in \partial kP}\frac {m(p;k)kf(p)}{(n)!(n+1)}+\textrm{Vol}(kP)\frac {f(0)}{(n+1)} \end{equation*}
and
do not hold in general. However, suppose there exists a positive integer
![]() $c$
such that
$c$
such that
 \begin{equation*}P=\bigcap _{i=1}^M\{l_i(x)\leqslant c\},\end{equation*}
\begin{equation*}P=\bigcap _{i=1}^M\{l_i(x)\leqslant c\},\end{equation*}
where
![]() $l_i(x)=a_i^1x_1+\cdots +a_i^nx_n$
are linear functions with integral coefficients such that
$l_i(x)=a_i^1x_1+\cdots +a_i^nx_n$
are linear functions with integral coefficients such that
![]() $(a_i^1,\ldots, a_i^n,c)$
are coprime. Then the inequalities become
$(a_i^1,\ldots, a_i^n,c)$
are coprime. Then the inequalities become
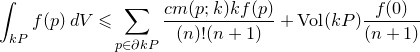 \begin{equation*}\int _{kP} f(p)\, dV \leqslant \sum _{p\in \partial kP}\frac {cm(p;k)kf(p)}{(n)!(n+1)}+\textrm{Vol}(kP)\frac {f(0)}{(n+1)} \end{equation*}
\begin{equation*}\int _{kP} f(p)\, dV \leqslant \sum _{p\in \partial kP}\frac {cm(p;k)kf(p)}{(n)!(n+1)}+\textrm{Vol}(kP)\frac {f(0)}{(n+1)} \end{equation*}
and
Then, by the same calculation as in the proof of Theorem 8.1, if we have other assumptions in Theorem 8.1, then the result still holds.
8.1
 $D(X_8)$
and
$D(X_8)$
and
 $D(X_9)$
$D(X_9)$
Recall that
![]() $D(X_8)$
and
$D(X_8)$
and
![]() $D(X_9)$
are given by
$D(X_9)$
are given by
In Example 4.8, we showed that
![]() $D(X_8)$
and
$D(X_8)$
and
![]() $D(X_9)$
are not special. Therefore, to show that
$D(X_9)$
are not special. Therefore, to show that
![]() $D(X_8)$
and
$D(X_8)$
and
![]() $D(X_9)$
are asymptotically Chow polystable, we have to triangulate the whole polytopes and compute the inequality directly.
$D(X_9)$
are asymptotically Chow polystable, we have to triangulate the whole polytopes and compute the inequality directly.
Notice that the only way to triangulate
![]() $D(X_8)$
and
$D(X_8)$
and
![]() $D(X_9)$
into simplices is the following. We triangulate
$D(X_9)$
into simplices is the following. We triangulate
![]() $X_8$
and
$X_8$
and
![]() $X_9$
as follows.
$X_9$
as follows.

Then we connect any small triangle to
![]() $(0,0,1)$
and
$(0,0,1)$
and
![]() $(0,0,-1)$
to get 3-simplex. Therefore, we can triangulate
$(0,0,-1)$
to get 3-simplex. Therefore, we can triangulate
![]() $D(X_8)$
into 16 simplices and
$D(X_8)$
into 16 simplices and
![]() $D(X_9)$
into 18 simplices. Then, by triangulation of each simplex, we have a triangulation of
$D(X_9)$
into 18 simplices. Then, by triangulation of each simplex, we have a triangulation of
![]() $kD(X_8)$
and
$kD(X_8)$
and
![]() $kD(X_9)$
.
$kD(X_9)$
.
As a consequence of Lemma 7.1, we have the following lemma.
Lemma 8.3.
For
![]() $kD(X_i)$
, under the above triangulation,
$kD(X_i)$
, under the above triangulation,
 \begin{equation*}n(p) \left \{ \begin{array}{cl} =i &\text { if } p=(0,0, \pm k),\\ \leqslant 24 & \text { if } p\in kD(X_i)^o,\\ \leqslant 12 & \text { if } p\in \partial kD(X_i). \end{array}\right . \end{equation*}
\begin{equation*}n(p) \left \{ \begin{array}{cl} =i &\text { if } p=(0,0, \pm k),\\ \leqslant 24 & \text { if } p\in kD(X_i)^o,\\ \leqslant 12 & \text { if } p\in \partial kD(X_i). \end{array}\right . \end{equation*}
Moreover, the triangulation on
![]() $kT_2$
combined with the induced triangulation on
$kT_2$
combined with the induced triangulation on
![]() $D(X_i)$
onto
$D(X_i)$
onto
![]() $\partial kD(X_i)$
gives
$\partial kD(X_i)$
gives
As a remark, for each
![]() $D(X_i)$
,
$D(X_i)$
,
![]() $n_{kP}(0,\ldots, 0)=2i$
, also for the triangulation of
$n_{kP}(0,\ldots, 0)=2i$
, also for the triangulation of
![]() $\partial kD_i$
,
$\partial kD_i$
,
![]() $n(p)=4$
for
$n(p)=4$
for
![]() $p \in \partial kP$
intersect with the red line.
$p \in \partial kP$
intersect with the red line.
Corollary 8.4.
For
![]() $i=3,4,6,8,9$
,
$i=3,4,6,8,9$
,
![]() $D(X_i)$
are asymptotically Chow polystable.
$D(X_i)$
are asymptotically Chow polystable.
Proof.
For
![]() $p \in \partial kP$
such that
$p \in \partial kP$
such that
![]() $p\neq (0,\ldots, \pm 1)$
,
$p\neq (0,\ldots, \pm 1)$
,
![]() $n(p;k)\leqslant \frac {(n+1)!}{2}$
and
$n(p;k)\leqslant \frac {(n+1)!}{2}$
and
![]() $m(p;k)\leqslant n!$
, the inequality becomes
$m(p;k)\leqslant n!$
, the inequality becomes
which is true. Also, at
![]() $p=(0,\ldots, 0, \pm 1)$
, we have
$p=(0,\ldots, 0, \pm 1)$
, we have
and then we need
That is,
If
![]() $n=3$
, then it becomes
$n=3$
, then it becomes
and hence this inequality holds for
![]() $i\leqslant 9$
. Therefore, by Lemma 8.3 and Theorem 8.1, for
$i\leqslant 9$
. Therefore, by Lemma 8.3 and Theorem 8.1, for
![]() $i=3,4,6,8,9$
,
$i=3,4,6,8,9$
,
![]() $D(X_i)$
are asymptotically Chow polystable.
$D(X_i)$
are asymptotically Chow polystable.
9. Examples of the stability of symmetric reflexive polytopes
9.1 One- and two-dimensional symmetric reflexive polytopes
Example 9.1.
The only one-dimensional symmetric reflexive polytope is
![]() $[-1,1]$
, which is Chow stable (see [Reference Lee, Li, Sturm and WangLLSW19]).
$[-1,1]$
, which is Chow stable (see [Reference Lee, Li, Sturm and WangLLSW19]).
Example 9.2.
Suppose
![]() $P$
is a two-dimensional symmetric reflexive polytope, so then it is special, and hence it is asymptotic Chow stable. Indeed, by Theorem 1.2 and Corollary 3.3 in [Reference Lee, Li, Sturm and WangLLSW19], combined with the fact that
$P$
is a two-dimensional symmetric reflexive polytope, so then it is special, and hence it is asymptotic Chow stable. Indeed, by Theorem 1.2 and Corollary 3.3 in [Reference Lee, Li, Sturm and WangLLSW19], combined with the fact that
![]() $\mathbb {P}^2$
and
$\mathbb {P}^2$
and
![]() $\mathbb {P}^1\times \mathbb {P}^1$
(by Proposition
3.2
) are Chow stable, so indeed, all two-dimensional special polytopes are Chow stable.
$\mathbb {P}^1\times \mathbb {P}^1$
(by Proposition
3.2
) are Chow stable, so indeed, all two-dimensional special polytopes are Chow stable.
As a remark, they are given by
and all the line bundles to define the polytopes are
![]() $-K_{X_i}$
. The polytopes are given in Figure 4.
$-K_{X_i}$
. The polytopes are given in Figure 4.

Figure 4.
![]() $X_i$
for
$X_i$
for
![]() $i=3,4,6,8,9$
.
$i=3,4,6,8,9$
.
Notice that in [Reference Lee, Li, Sturm and WangLLSW19] there are some examples of the non-reflexive polytopes which we will not discuss in detail in this note.
9.2 Three-dimensional polytopes
To study the higher-dimensional polytopes, we first recall that, given a reflexive polytope
![]() $P$
, we can define the dual polytope
$P$
, we can define the dual polytope
![]() $\hat {P}$
as follows. Let
$\hat {P}$
as follows. Let
If
![]() $P$
is symmetric and reflexive, so is
$P$
is symmetric and reflexive, so is
![]() $\hat {P}$
. For example,
$\hat {P}$
. For example,
![]() $D(P)=\widehat {\hat {P}\times \mathbb {P}^1}$
. However, the duality may not share the stability.
$D(P)=\widehat {\hat {P}\times \mathbb {P}^1}$
. However, the duality may not share the stability.
By Lemma 7.1, for faces that are 2-simplices or rectangles, then
![]() $m(p)=6$
for
$m(p)=6$
for
![]() $p\in P^o$
,
$p\in P^o$
,
![]() $m(p)=3$
if
$m(p)=3$
if
![]() $p\in (\partial P)^o$
, and
$p\in (\partial P)^o$
, and
![]() $m(p)=1$
if
$m(p)=1$
if
![]() $p$
is the vertex. For any
$p$
is the vertex. For any
![]() $p\in (\partial P)^o$
, there are at most two faces connected to
$p\in (\partial P)^o$
, there are at most two faces connected to
![]() $p$
, so in order to check if a polytope is special, we only need that there are
$p$
, so in order to check if a polytope is special, we only need that there are
![]() $i\leqslant 6$
simplices connecting each vertex under the triangulation on the boundary.
$i\leqslant 6$
simplices connecting each vertex under the triangulation on the boundary.
Denote
![]() $\Delta _0$
as the triangulation of a 2-simplex. As in Figure 5, if the faces are given by
$\Delta _0$
as the triangulation of a 2-simplex. As in Figure 5, if the faces are given by
![]() $X_i$
, for
$X_i$
, for
![]() $i=3,4,6$
, then
$i=3,4,6$
, then
![]() $n(0)=i$
,
$n(0)=i$
,
![]() $n(p)=6$
for
$n(p)=6$
for
![]() $p\in P^o-\{0\}$
,
$p\in P^o-\{0\}$
,
![]() $n(p)=3$
if
$n(p)=3$
if
![]() $p\in (\partial P)^o$
, and
$p\in (\partial P)^o$
, and
![]() $n(p)=2$
if
$n(p)=2$
if
![]() $p$
is the vertex using the rotation of
$p$
is the vertex using the rotation of
![]() $\Delta _0$
as the triangulation.
$\Delta _0$
as the triangulation.

Figure 5.
![]() $\triangle _0\subset X_3$
,
$\triangle _0\subset X_3$
,
![]() $\triangle _0\subset X_4$
and
$\triangle _0\subset X_4$
and
![]() $\triangle _0\subset X_6$
.
$\triangle _0\subset X_6$
.
Therefore, if the polytopes whose faces are a combination of the above, then the only possible problem is the vertex, and we can study those polytopes case by case.

Figure 6.
![]() $X_i \times [-1,1]$
.
$X_i \times [-1,1]$
.

Figure 7.
![]() $D(X_i)$
.
$D(X_i)$
.

Figure 8. Other special polytopes, where the red line indicates part of the triangulation.
Proposition 9.3. The following symmetric reflexive three-dimensional polytopes are asymptotically chow polystable.
-
(i)
 $X_i\times [-1,1]$
for
$X_i\times [-1,1]$
for
 $i=3,4,6,8,9$
(Figure 6).
$i=3,4,6,8,9$
(Figure 6). -
(ii)
 $D(X_i)$
, where
$D(X_i)$
, where
 $i=3,4,6,8,9$
(Figure 7).
$i=3,4,6,8,9$
(Figure 7). -
(iii) Other polytopes (Figure 8):
-
(a) the polytope of
 $(\mathbb {P}^3, O(4)):=\textrm{conv}\{(-1,-1,-1), (3,-1,-1),(-1,3,-1), (-1,-1,3)\}$
(tetrahedron) and its dual,
$(\mathbb {P}^3, O(4)):=\textrm{conv}\{(-1,-1,-1), (3,-1,-1),(-1,3,-1), (-1,-1,3)\}$
(tetrahedron) and its dual,
 $A_3=\textrm{conv}\{(-1,-1,-1), (1,0,0), (0,1,0),(0,0,1)\}$
(tetrahedron;
$A_3=\textrm{conv}\{(-1,-1,-1), (1,0,0), (0,1,0),(0,0,1)\}$
(tetrahedron;
-
(b) the polytope of
 $\mathbb {P}^3$
blow up 4 points, which is a convex set of the points
$\mathbb {P}^3$
blow up 4 points, which is a convex set of the points
 $(0,-1,-1),\ (-1,0,-1),\ (-1,-1,0),\ (2,-1,-1),\ (2,-1,0),\ (2,0,-1),\ (-1,2,-1)$
,
$(0,-1,-1),\ (-1,0,-1),\ (-1,-1,0),\ (2,-1,-1),\ (2,-1,0),\ (2,0,-1),\ (-1,2,-1)$
,
 $ (-1,2,0), (0,2,-1), (-1,-1,2), (-1,0,2), (0,-1,2)$
. Hence this polytope is a truncated tetrahedron, in which the boundaries contain 4
$ (-1,2,0), (0,2,-1), (-1,-1,2), (-1,0,2), (0,-1,2)$
. Hence this polytope is a truncated tetrahedron, in which the boundaries contain 4
 $X_6$
and 4-simplices. Each vertex is connected with one 2-simplex and two
$X_6$
and 4-simplices. Each vertex is connected with one 2-simplex and two
 $X_6$
; and its dual:
$X_6$
; and its dual:
-
(c) The dual polytope of (B),
 $\textrm{conv}\{(\pm 1, 0, 0) (0,\pm 1, 0), (0, 0, \pm 1), (-1,-1,-1),(1,1,1)\}$
, which is
$\textrm{conv}\{(\pm 1, 0, 0) (0,\pm 1, 0), (0, 0, \pm 1), (-1,-1,-1),(1,1,1)\}$
, which is
 $D(X_4)$
glue with two standard 3-simplices, and the faces are all standard 2-simplices.
$D(X_4)$
glue with two standard 3-simplices, and the faces are all standard 2-simplices.
-
(d) The polytope
 $\textrm{conv}\{{\kern-1pt} (\pm 1,0, 0{\kern-.2pt}),(0, \pm 1, 0{\kern-.2pt}), (\pm 1, \mp 1, 0{\kern-.2pt}), (0, 0, \pm 1{\kern-.2pt}), (\pm 1, 0, \mp 1{\kern-.2pt}), (0, \pm 1, \mp 1{\kern-.2pt}){\kern-1pt}\}$
, which is a cuboctahedron, with eight triangular faces and six square faces, and each vertex is connected to two 2-simplex and 2-square, and its dual, which is given by:
$\textrm{conv}\{{\kern-1pt} (\pm 1,0, 0{\kern-.2pt}),(0, \pm 1, 0{\kern-.2pt}), (\pm 1, \mp 1, 0{\kern-.2pt}), (0, 0, \pm 1{\kern-.2pt}), (\pm 1, 0, \mp 1{\kern-.2pt}), (0, \pm 1, \mp 1{\kern-.2pt}){\kern-1pt}\}$
, which is a cuboctahedron, with eight triangular faces and six square faces, and each vertex is connected to two 2-simplex and 2-square, and its dual, which is given by:
-
(e) the convex hull of the points:
which is a rhombic dodecahedron. \begin{gather*}(1,0,0),(1,1,0),(0,1,0),(-1,0,0),(-1,-1,0), (0,-1,0), \\(0,0,1),(1,0,1),(1,1,1), (0,1,1), (0,0,-1),(-1,0,-1),(-1,-1,-1), (0,-1,-1), \end{gather*}
\begin{gather*}(1,0,0),(1,1,0),(0,1,0),(-1,0,0),(-1,-1,0), (0,-1,0), \\(0,0,1),(1,0,1),(1,1,1), (0,1,1), (0,0,-1),(-1,0,-1),(-1,-1,-1), (0,-1,-1), \end{gather*}
-
Proof.
-
(i)
 $X_i\times [-1,1]$
for
$X_i\times [-1,1]$
for
 $i=3,4,6,8,9$
: All two-dimensional reflexive symmetric polytopes are special, and hence
$i=3,4,6,8,9$
: All two-dimensional reflexive symmetric polytopes are special, and hence
 $X_i$
are asymptotically chow polystable. Also, as stated in Example 9.1,
$X_i$
are asymptotically chow polystable. Also, as stated in Example 9.1,
 $[-1,1]$
is asymptotically chow polystable. By Proposition 3.2, they are asymptotically chow polystable.
$[-1,1]$
is asymptotically chow polystable. By Proposition 3.2, they are asymptotically chow polystable. -
(ii)
 $D(X_i)$
, where
$D(X_i)$
, where
 $i=3,4,6,8,9$
: This is a direct consequence of Corollary 8.4.
$i=3,4,6,8,9$
: This is a direct consequence of Corollary 8.4. -
(iii) To show the remaining polytopes are asymptotically Chow polystable, we only need to show that the remaining polytopes are special. As we explained right before this statement, if the faces of the boundary consist of
 $X_i$
for
$X_i$
for
 $i=3,4,6$
, 2-simplices and rectangles, then
$i=3,4,6$
, 2-simplices and rectangles, then
 $m_k(p)\leqslant 6$
for all non-vertexes
$m_k(p)\leqslant 6$
for all non-vertexes
 $p$
. Also, for any vertex
$p$
. Also, for any vertex
 $p$
, denote
$p$
, denote
 $N(S)$
to be the number of
$N(S)$
to be the number of
 $S$
connected to
$S$
connected to
 $p$
, so thenwhere
$p$
, so thenwhere \begin{equation*}m_k(p)=\sum _{i=3,4,6}2 N(X_i)+ N(\text {2 simplices})+a N(\text {rectangles}),\end{equation*}
\begin{equation*}m_k(p)=\sum _{i=3,4,6}2 N(X_i)+ N(\text {2 simplices})+a N(\text {rectangles}),\end{equation*}
 $a$
can be 1 or 2 depending on the triangulation. In particular, if all the faces of the boundary are given by
$a$
can be 1 or 2 depending on the triangulation. In particular, if all the faces of the boundary are given by
 $X_3,X_4,X_6$
, simplices or rectangles, and the number of faces connected to a vertex
$X_3,X_4,X_6$
, simplices or rectangles, and the number of faces connected to a vertex
 $p$
is smaller than 3, then
$p$
is smaller than 3, then
 $m_k(p)\leqslant 6$
. Also, see Figures 8 in § 10, which provide the detail of the boundary of the polytopes.
$m_k(p)\leqslant 6$
. Also, see Figures 8 in § 10, which provide the detail of the boundary of the polytopes.-
(a) The polytope of
 $(\mathbb {P}^3, O(4)):=\textrm{conv}\{(-1,-1,-1), (3,-1,-1),(-1,3,-1), (-1,-1,3)\}$
. The boundary consists of four enlarged two-dimensional simplices, hence
$(\mathbb {P}^3, O(4)):=\textrm{conv}\{(-1,-1,-1), (3,-1,-1),(-1,3,-1), (-1,-1,3)\}$
. The boundary consists of four enlarged two-dimensional simplices, hence
 $m_k(p)\leqslant 6$
, and for all the vertexes
$m_k(p)\leqslant 6$
, and for all the vertexes
 $p$
,
$p$
,
 $m_k(p)=3$
. For
$m_k(p)=3$
. For
 $A_3=\textrm{conv}\{(-1,-1,-1), (1,0,0), (0,1,0),(0,0,1)\}$
, the boundary consists of 4
$A_3=\textrm{conv}\{(-1,-1,-1), (1,0,0), (0,1,0),(0,0,1)\}$
, the boundary consists of 4
 $X_3$
. Also, each vertex
$X_3$
. Also, each vertex
 $p$
is connected to 3
$p$
is connected to 3
 $X_3$
, and henceTherefore,
$X_3$
, and henceTherefore, \begin{equation*}m_k(p)=6.\end{equation*}
\begin{equation*}m_k(p)=6.\end{equation*}
 $A_3$
is special.
$A_3$
is special.
-
(b) The convex set of the points
 $(0,-1,-1),(-1,0,-1), (-1,-1,0). (2,-1,-1),(2,-1,0) $
,
$(0,-1,-1),(-1,0,-1), (-1,-1,0). (2,-1,-1),(2,-1,0) $
,
 $(2,0,-1), (-1,2,-1),(-1,2,0), (0,2,-1), (-1,-1,2), (-1,0,2), (0,-1,2)$
is a truncated tetrahedron, in which the boundary contains four
$(2,0,-1), (-1,2,-1),(-1,2,0), (0,2,-1), (-1,-1,2), (-1,0,2), (0,-1,2)$
is a truncated tetrahedron, in which the boundary contains four
 $X_6$
and four 2-simplices. Each vertex is connected with 2 simplices and 2
$X_6$
and four 2-simplices. Each vertex is connected with 2 simplices and 2
 $X_6$
, so for any vertex
$X_6$
, so for any vertex
 $p$
,The symmetric group acting on it is the permutation group
$p$
,The symmetric group acting on it is the permutation group \begin{equation*}m_k(p)=2+2\times 2=6.\end{equation*}
\begin{equation*}m_k(p)=2+2\times 2=6.\end{equation*}
 $S_4$
, which is the induced action from the permutation of the vertexes of the enlarged simplex, and hence it is symmetric. Also, by Figures 8 in § 10, we can see that it is reflexive. So, it is special.
$S_4$
, which is the induced action from the permutation of the vertexes of the enlarged simplex, and hence it is symmetric. Also, by Figures 8 in § 10, we can see that it is reflexive. So, it is special.
-
(c)
which is \begin{equation*}\textrm{conv}\{(\pm 1, 0, 0) (0,\pm 1, 0), (0, 0, \pm 1), (-1,-1,-1),(1,1,1)\},\end{equation*}
\begin{equation*}\textrm{conv}\{(\pm 1, 0, 0) (0,\pm 1, 0), (0, 0, \pm 1), (-1,-1,-1),(1,1,1)\},\end{equation*}
 $D(X_4)$
glue with two standard 3-simplices, for which the faces are all standard 2-simplices. By Figure 8 in § 10, we can see that the number of faces connected to each vertex is less than six, the symmetric group acting on it is the permutation group
$D(X_4)$
glue with two standard 3-simplices, for which the faces are all standard 2-simplices. By Figure 8 in § 10, we can see that the number of faces connected to each vertex is less than six, the symmetric group acting on it is the permutation group
 $S_4$
, and it is reflexive. So it is special.
$S_4$
, and it is reflexive. So it is special.
-
(d)
 $\textrm{conv}\{ (\pm 1,0, 0),(0, \pm 1, 0), (\pm 1, \mp 1, 0), (0, 0, \pm 1), (\pm 1, 0, \mp 1), (0, \pm 1, \mp 1)\}$
, which is a cuboctahedron, with eight triangular faces and six square faces, and each vertex is connected to one 2-simplices and two squares. Hence, for the surface, and for each vertex
$\textrm{conv}\{ (\pm 1,0, 0),(0, \pm 1, 0), (\pm 1, \mp 1, 0), (0, 0, \pm 1), (\pm 1, 0, \mp 1), (0, \pm 1, \mp 1)\}$
, which is a cuboctahedron, with eight triangular faces and six square faces, and each vertex is connected to one 2-simplices and two squares. Hence, for the surface, and for each vertex
 $p$
,Also, the group acting on the polytope contains
$p$
,Also, the group acting on the polytope contains \begin{equation*}m_k(p)\leqslant 2+2 \cdot 2=6.\end{equation*}
\begin{equation*}m_k(p)\leqslant 2+2 \cdot 2=6.\end{equation*}
 $\mathbb {Z}_3\times \mathbb {Z}_2$
, the rotation group rotates along the z-axis, times the reflection group
$\mathbb {Z}_3\times \mathbb {Z}_2$
, the rotation group rotates along the z-axis, times the reflection group
 $\{\textrm{id}, \sigma \}$
, which
$\{\textrm{id}, \sigma \}$
, which
 $\sigma (p)=-p$
. Therefore this polytope is symmetric. Also, from Figure 8 in § 10, we can see it is reflexive. Therefore, it is special, and its dual, which is given by
$\sigma (p)=-p$
. Therefore this polytope is symmetric. Also, from Figure 8 in § 10, we can see it is reflexive. Therefore, it is special, and its dual, which is given by
-
(e) the convex hull of the points,
is a rhombic dodecahedron. This is symmetric as the symmetric group is the same as its dual. By Figures 8 in § 10, we can see that it is reflexive. Also, the vertices \begin{gather*}(1,0,0),(1,1,0),(0,1,0),(-1,0,0),(-1,-1,0), (0,-1,0), \\(0,0,1),(1,0,1),(1,1,1), (0,1,1), (0,0,-1),(-1,0,-1),(-1,-1,-1), (0,-1,-1), \end{gather*}
\begin{gather*}(1,0,0),(1,1,0),(0,1,0),(-1,0,0),(-1,-1,0), (0,-1,0), \\(0,0,1),(1,0,1),(1,1,1), (0,1,1), (0,0,-1),(-1,0,-1),(-1,-1,-1), (0,-1,-1), \end{gather*}
 $(0,1,1), (1,0,1), (0,-1,-1),(-1,0,-1)$
have four squares touching the points, and the others have only three. So when we triangulate the surface, if we choose the triangulation such that two of the squares do not bisect along those points, then for any point
$(0,1,1), (1,0,1), (0,-1,-1),(-1,0,-1)$
have four squares touching the points, and the others have only three. So when we triangulate the surface, if we choose the triangulation such that two of the squares do not bisect along those points, then for any point
 $p$
in it,and hence this polytope is special. (See § 10 for the above triangulation.)
$p$
in it,and hence this polytope is special. (See § 10 for the above triangulation.) \begin{equation*}m_k(p)\leqslant 6,\end{equation*}
\begin{equation*}m_k(p)\leqslant 6,\end{equation*}
-
Remark 9.4. Indeed, except for
![]() $D(X_8)$
and
$D(X_8)$
and
![]() $D(X_9)$
, all the polytopes given in Proposition 9.3 are special. Also, we conjecture that all three-dimensional symmetric reflexive polytopes are asymptotically Chow polystable, and they are special except
$D(X_9)$
, all the polytopes given in Proposition 9.3 are special. Also, we conjecture that all three-dimensional symmetric reflexive polytopes are asymptotically Chow polystable, and they are special except
![]() $D(X_8)$
and
$D(X_8)$
and
![]() $D(X_9)$
. The difficulty in showing this conjecture is to find all three-dimensional symmetric reflexive polytopes up to the integral isomorphism.
$D(X_9)$
. The difficulty in showing this conjecture is to find all three-dimensional symmetric reflexive polytopes up to the integral isomorphism.
9.3 Higher-dimensional polytopes
One knows that in high dimensions that not every symmetric reflexive polytope is asymptotic Chow stable, for example
![]() $ D([-1,1]^n)$
for
$ D([-1,1]^n)$
for
![]() $n\geqslant 6$
. On the other hand, we can provide two classes of polytopes that are special.
$n\geqslant 6$
. On the other hand, we can provide two classes of polytopes that are special.
Example 9.5.
Consider
![]() $A_n:=\{[z_0,\ldots, z_{n+1}]\in \mathbb {P}^{n+1}\mid z_1\ldots z_{n+1}=z_{0}^{n+1}\}$
. The corresponding polytopes, also denoted as
$A_n:=\{[z_0,\ldots, z_{n+1}]\in \mathbb {P}^{n+1}\mid z_1\ldots z_{n+1}=z_{0}^{n+1}\}$
. The corresponding polytopes, also denoted as
![]() $A_n$
, are given by
$A_n$
, are given by
As all the faces of
![]() $A_n$
are simplices, with all the codimension 2 or above boundary intersecting with less than
$A_n$
are simplices, with all the codimension 2 or above boundary intersecting with less than
![]() $n$
, it is asymptotic Chow polystable.
$n$
, it is asymptotic Chow polystable.
Notice that
![]() $A_2= X_3$
in our notation on symmetric reflexive polygons. Also, as a polytope, each
$A_2= X_3$
in our notation on symmetric reflexive polygons. Also, as a polytope, each
![]() $A_n$
is the dual polytope of the polytope corresponding to
$A_n$
is the dual polytope of the polytope corresponding to
![]() $(\mathbb {P}^n, O(n+1))$
.
$(\mathbb {P}^n, O(n+1))$
.
To show
![]() $A_n$
are special for all
$A_n$
are special for all
![]() $n\geqslant 3$
, notice that the boundry of
$n\geqslant 3$
, notice that the boundry of
![]() $A_n$
is given by
$A_n$
is given by
![]() $n$
piece of
$n$
piece of
![]() $(n-1)$
-simplices. So we only need to know how many simplicies will be attached to a point in the codimension k skeleton.
$(n-1)$
-simplices. So we only need to know how many simplicies will be attached to a point in the codimension k skeleton.
Let
![]() $a_i=e_i$
and
$a_i=e_i$
and
![]() $a_{n-1}= (-1,\ldots, -1)$
, so then we can represent any codimensional k piece by the following:
$a_{n-1}= (-1,\ldots, -1)$
, so then we can represent any codimensional k piece by the following:
![]() $a_1$
represents the point
$a_1$
represents the point
![]() $e_1$
,
$e_1$
,
![]() $\{a_1,a_2\}$
represents the segment containing
$\{a_1,a_2\}$
represents the segment containing
![]() $a_1,a_2$
, etc. Also, as the symmetric group
$a_1,a_2$
, etc. Also, as the symmetric group
![]() $S_{n+1}$
acts on
$S_{n+1}$
acts on
![]() $A_n$
, we only need to consider how many faces contain the
$A_n$
, we only need to consider how many faces contain the
![]() $n-r$
skeleton
$n-r$
skeleton
![]() $\{a_1\ldots a_{n-r}\}$
. But the faces containing
$\{a_1\ldots a_{n-r}\}$
. But the faces containing
![]() $a_1\ldots a_{n-r}$
are represented by the set
$a_1\ldots a_{n-r}$
are represented by the set
![]() $\{a_{n-r+1}\ldots a_{n+1}\}$
removing one element. Therefore, there are
$\{a_{n-r+1}\ldots a_{n+1}\}$
removing one element. Therefore, there are
![]() $r+1$
faces connecting the skeleton containing
$r+1$
faces connecting the skeleton containing
![]() $a_1\ldots a_{n-r}$
. Therefore, Lemma 7.1 implies that, for any point
$a_1\ldots a_{n-r}$
. Therefore, Lemma 7.1 implies that, for any point
![]() $p\in \partial kP$
which is in the interior of the
$p\in \partial kP$
which is in the interior of the
![]() $n-r$
skeleton,
$n-r$
skeleton,
Therefore,
![]() $A_n$
has a regular triangulation. Also, all
$A_n$
has a regular triangulation. Also, all
![]() $A_n$
are symmetric and reflexive, and hence they are special, which implies all
$A_n$
are symmetric and reflexive, and hence they are special, which implies all
![]() $A_n$
for
$A_n$
for
![]() $n\geqslant 2$
are asymptotically Chow polystable.
$n\geqslant 2$
are asymptotically Chow polystable.
Example 9.6.
Consider
![]() $(\mathbb {P}^n, O(n+1))$
. The boundary of
$(\mathbb {P}^n, O(n+1))$
. The boundary of
![]() $k(\mathbb {P}^n, O(n+1))$
is defined by
$k(\mathbb {P}^n, O(n+1))$
is defined by
 \begin{equation*}\bigcap _{i=1}^n\{x_i=-k\}\cap \{x_1+\cdots + x_n=k\}.\end{equation*}
\begin{equation*}\bigcap _{i=1}^n\{x_i=-k\}\cap \{x_1+\cdots + x_n=k\}.\end{equation*}
Up to an
![]() $S_{n+1}$
action, a point
$S_{n+1}$
action, a point
![]() $p$
is in the interior of a codimensional
$p$
is in the interior of a codimensional
![]() $r$
skeleton if
$r$
skeleton if
where
![]() $v\in \mathbb {R}^{n-r}$
such that
$v\in \mathbb {R}^{n-r}$
such that
for all
![]() $i=1,\ldots, n-k$
. Hence
$i=1,\ldots, n-k$
. Hence
![]() $n(p)=r$
. So we have the same calculation of
$n(p)=r$
. So we have the same calculation of
![]() $A_n$
, which implies it is special, and therefore it is asymptotically Chow polystable.
$A_n$
, which implies it is special, and therefore it is asymptotically Chow polystable.
Example 9.7.
Define
![]() $D_n:=\textrm{conv}\{(\pm 1,\ldots, 0), (0, \pm 1, 0,\ldots, 0), \ldots, (0,\ldots, 0, \pm 1) \}$
so
$D_n:=\textrm{conv}\{(\pm 1,\ldots, 0), (0, \pm 1, 0,\ldots, 0), \ldots, (0,\ldots, 0, \pm 1) \}$
so
![]() $D_n$
is special for all
$D_n$
is special for all
![]() $n$
. Notice that
$n$
. Notice that
![]() $D_2=X_4$
and
$D_2=X_4$
and
![]() $D_3= D(X_4)$
.
$D_3= D(X_4)$
.
Proof.
Notice that
![]() $k D_n=\mathbb {Z}_2^n \cdot kT_n$
, where
$k D_n=\mathbb {Z}_2^n \cdot kT_n$
, where
![]() $\mathbb {Z}_2^n=\{1,-1\}^n$
with the group action to be multiplication, and the action is multiplication to the corresponding coordinate.
$\mathbb {Z}_2^n=\{1,-1\}^n$
with the group action to be multiplication, and the action is multiplication to the corresponding coordinate.
![]() $D_n$
is symmetric and reflexive. To show that
$D_n$
is symmetric and reflexive. To show that
![]() $D_n$
has a regular boundary,
$D_n$
has a regular boundary,
![]() $p$
is in the interior of the codimension
$p$
is in the interior of the codimension
![]() $r+1$
skeleton if
$r+1$
skeleton if
![]() $p=(x_1,\ldots, x_n) \in \partial k D_n$
with
$p=(x_1,\ldots, x_n) \in \partial k D_n$
with
for
![]() $r=0,\ldots, n-1$
. We denote these points as
$r=0,\ldots, n-1$
. We denote these points as
![]() $p_r$
. Hence, similar to Example 9.6, as a consequence of Lemma 7.1, we have
$p_r$
. Hence, similar to Example 9.6, as a consequence of Lemma 7.1, we have
and hence
![]() $D_n$
is special.
$D_n$
is special.
Example 9.8.
Notice that
![]() $D_6$
is the dual polytope of
$D_6$
is the dual polytope of
![]() $[-1,1]^6$
, and thus
$[-1,1]^6$
, and thus
![]() $D_6\times [-1,1]$
(i.e.
$D_6\times [-1,1]$
(i.e.
![]() $D_6\times \mathbb {P}^1$
as the corresponding variety) is asymptotically Chow polystable. However, its dual is
$D_6\times \mathbb {P}^1$
as the corresponding variety) is asymptotically Chow polystable. However, its dual is
![]() $D([-1,1]^6)$
; therefore, a dual of an asymptotically Chow polystable polytope need not be asymptotically Chow polystable (or even semistable).
$D([-1,1]^6)$
; therefore, a dual of an asymptotically Chow polystable polytope need not be asymptotically Chow polystable (or even semistable).
Appendix A. From integral polytypes to varieties
In this appendix, we will briefly explain how we obtain a toric variety from an integral polytope. Then we will write down the corresponding varieties of the toric varieties occurring in this note.
A.1 General procedure
Let
![]() $P$
be a integral polytope containing
$P$
be a integral polytope containing
![]() $(0,\ldots, 0)$
. Let
$(0,\ldots, 0)$
. Let
![]() $\{p_0=(0,\ldots, 0), p_1,\ldots, p_{N}\}$
be all the integral points in
$\{p_0=(0,\ldots, 0), p_1,\ldots, p_{N}\}$
be all the integral points in
![]() $P$
. Then we can define a toric subvariety in
$P$
. Then we can define a toric subvariety in
![]() $\mathbb {P}^N$
by the following equations.
$\mathbb {P}^N$
by the following equations.
Suppose we have
and without loss of generality, we may assume
for some
![]() $a \geqslant 0$
. Then we have a homogeneous polynomial defined by
$a \geqslant 0$
. Then we have a homogeneous polynomial defined by
Then the zero set
![]() $\{[z_0,\ldots z_N]\in \mathbb {P}^N\mid z_{i_1}^{c_1}\cdots z_{i_r}^{c_r}- z_{j_1}^{b_1}\cdots z_{j_s}^{b_s}z_0^a=0\}$
is a divisor in
$\{[z_0,\ldots z_N]\in \mathbb {P}^N\mid z_{i_1}^{c_1}\cdots z_{i_r}^{c_r}- z_{j_1}^{b_1}\cdots z_{j_s}^{b_s}z_0^a=0\}$
is a divisor in
![]() $\mathbb {P}^{N}$
, and it is a toric subvariety.The toric action is given by
$\mathbb {P}^{N}$
, and it is a toric subvariety.The toric action is given by
By intersecting all these divisors, we can obtain a toric subvariety.
Notice that some of the equations are repeated in
![]() $({\mathbb {C}}^*)^N$
, so in the following we will define the variety only by those which are different equations in
$({\mathbb {C}}^*)^N$
, so in the following we will define the variety only by those which are different equations in
![]() $({\mathbb {C}}^*)^N$
, and the variety is the closure of this.
$({\mathbb {C}}^*)^N$
, and the variety is the closure of this.
A.2 Examples
Example A.1 (
![]() $A_n$
). Denote
$A_n$
). Denote
![]() $p_0=(0,\ldots, 0)$
,
$p_0=(0,\ldots, 0)$
,
![]() $p_i=e_i$
for
$p_i=e_i$
for
![]() $i=1,\ldots, n$
and
$i=1,\ldots, n$
and
![]() $p_{n+1}=(-1,\ldots, -1)$
. Then we have
$p_{n+1}=(-1,\ldots, -1)$
. Then we have
so the corresponding varieties, also denoted as
![]() $A_n$
, are given by
$A_n$
, are given by
Example A.2 (
![]() $D_n$
). Recall that
$D_n$
). Recall that
![]() $D_n:=\textrm{conv}\{\pm e_i\}$
. Denote
$D_n:=\textrm{conv}\{\pm e_i\}$
. Denote
![]() $p_0=(0,\ldots, 0)$
,
$p_0=(0,\ldots, 0)$
,
![]() $p_{2i-1}=e_i$
,
$p_{2i-1}=e_i$
,
![]() $p_{2i}=-e_i$
for
$p_{2i}=-e_i$
for
![]() $i=1,\ldots, n$
. Then
$i=1,\ldots, n$
. Then
![]() $p_{2i-1}+p_{2i}=0$
for
$p_{2i-1}+p_{2i}=0$
for
![]() $i=1,\ldots, n$
gives
$i=1,\ldots, n$
gives
![]() $n$
equations
$n$
equations
![]() $z_{2i-1}z_{2i}=z_0^2$
, and it gives a
$z_{2i-1}z_{2i}=z_0^2$
, and it gives a
![]() $n$
codimension subvariety of
$n$
codimension subvariety of
![]() $\mathbb {P}^{2n}$
; hence these equations define
$\mathbb {P}^{2n}$
; hence these equations define
![]() $D_n$
,
$D_n$
,
Given
we denote
Example A.3 (
![]() $D(P)$
). Let
$D(P)$
). Let
![]() $P$
be defined by
$P$
be defined by
Then we define
![]() $\hat {f_i}(z_0,\ldots, z_{N+2})=f_i(z_0,\ldots, z_N)$
. Then by denoting
$\hat {f_i}(z_0,\ldots, z_{N+2})=f_i(z_0,\ldots, z_N)$
. Then by denoting
![]() $p_{N+1}=(0,\ldots, 0,1)$
,
$p_{N+1}=(0,\ldots, 0,1)$
,
![]() $p_{N+2}=(0,\ldots, 0,-1)$
, we have a new equation,
$p_{N+2}=(0,\ldots, 0,-1)$
, we have a new equation,
Then the variety of
![]() $D(P)$
is given by
$D(P)$
is given by
In order to define
![]() $D(P)$
, we need to know
$D(P)$
, we need to know
![]() $P$
as a subvariety of
$P$
as a subvariety of
![]() $\mathbb {P}^N$
. Therefore, in order to compute all the examples, we need to write down what
$\mathbb {P}^N$
. Therefore, in order to compute all the examples, we need to write down what
![]() $X_i$
is as a subvariety.
$X_i$
is as a subvariety.
Example A.4.
As a subvariety of
![]() $\mathbb {P}^i$
, restricted in
$\mathbb {P}^i$
, restricted in
![]() $({\mathbb {C}}^*)^i\subset \mathbb {P}^i$
,
$({\mathbb {C}}^*)^i\subset \mathbb {P}^i$
,
![]() $X_i$
are given by:
$X_i$
are given by:
-
(i)
 $X_3=A_2=\{[z_0,z_1,z_2,z_3]\in \mathbb {P}^3\mid z_1z_2z_3=z_0^3\}$
;
$X_3=A_2=\{[z_0,z_1,z_2,z_3]\in \mathbb {P}^3\mid z_1z_2z_3=z_0^3\}$
; -
(ii)
 $X_4=D_2=\{[z_0,z_1,z_2,z_3,z_4]\in \mathbb {P}^4\mid z_1z_2=z_0^2, z_3z_4=z_0^2\}$
;
$X_4=D_2=\{[z_0,z_1,z_2,z_3,z_4]\in \mathbb {P}^4\mid z_1z_2=z_0^2, z_3z_4=z_0^2\}$
; -
(iii)
 $X_6=\{[z_0,z_1,\ldots, z_6]\in \mathbb {P}^6\mid z_1z_4=z_2z_5=z_3z_6=z_0^2, z_2z_4=z_3z_0\}$
, where this last equation comes from
$X_6=\{[z_0,z_1,\ldots, z_6]\in \mathbb {P}^6\mid z_1z_4=z_2z_5=z_3z_6=z_0^2, z_2z_4=z_3z_0\}$
, where this last equation comes from
 $(0,1)+(-1,0)=(-1,1)$
and
$(0,1)+(-1,0)=(-1,1)$
and
 $z_2z_4=z_3z_0$
can be replaced by
$z_2z_4=z_3z_0$
can be replaced by
 $z_1z_3z_5=z_0^3$
with other equations to get the same variety;
$z_1z_3z_5=z_0^3$
with other equations to get the same variety;
-
(iv)
 $X_8=\{[z_0,z_1,\ldots, z_8]\in \mathbb {P}^8\mid z_rz_{r+4}=z_0^2, \text { where }r=1,2,3,4; z_1z_3=z_2z_0, z_3z_5=z_4z_0\}$
; and
$X_8=\{[z_0,z_1,\ldots, z_8]\in \mathbb {P}^8\mid z_rz_{r+4}=z_0^2, \text { where }r=1,2,3,4; z_1z_3=z_2z_0, z_3z_5=z_4z_0\}$
; and
-
(v)
 $X_9=\{[z_0,z_1,\ldots, z_9]\in \mathbb {P}^9\mid z_rz_{r+3}z_{r+6}=z_0^3, \text { where } r=1,2,3; z_1z_3=z_2^2, z_2z_4=z_3^2, z_2z_6=z_0^2,z_3z_7=z_0^2\}$
. Another way to write this uses
$X_9=\{[z_0,z_1,\ldots, z_9]\in \mathbb {P}^9\mid z_rz_{r+3}z_{r+6}=z_0^3, \text { where } r=1,2,3; z_1z_3=z_2^2, z_2z_4=z_3^2, z_2z_6=z_0^2,z_3z_7=z_0^2\}$
. Another way to write this uses
 $X_6$
plus 3 points, hence we need two more relations, namely
$X_6$
plus 3 points, hence we need two more relations, namely
 \begin{equation*}\{[z_0,z_1,\ldots, z_9]\in \mathbb {P}^9\mid z_1z_4=z_2z_5=z_3z_6=z_0^2, z_2z_4=z_3z_0, z_7z_8z_9=z_0^3, z_7z_8=z_1z_2\}.\end{equation*}
\begin{equation*}\{[z_0,z_1,\ldots, z_9]\in \mathbb {P}^9\mid z_1z_4=z_2z_5=z_3z_6=z_0^2, z_2z_4=z_3z_0, z_7z_8z_9=z_0^3, z_7z_8=z_1z_2\}.\end{equation*}
With this, we can write
![]() $D(X_i)$
as subvarieties of
$D(X_i)$
as subvarieties of
![]() $\mathbb {P}^{i+2}$
. For example,
$\mathbb {P}^{i+2}$
. For example,
-
(i)
 $D(X_3)=\{[z_0,z_1,z_2,z_3,z_4,z_5]\in \mathbb {P}^5\mid z_1z_2z_3=z_0^3,z_4z_5=z_0^2\}$
;
$D(X_3)=\{[z_0,z_1,z_2,z_3,z_4,z_5]\in \mathbb {P}^5\mid z_1z_2z_3=z_0^3,z_4z_5=z_0^2\}$
; -
(ii)
 $D(X_4)=\{[z_0,z_1,\ldots, z_6]\in \mathbb {P}^6\mid z_1z_2=z_0^2, z_3z_4=z_0^2,z_5z_6=z_0^2\}$
;
$D(X_4)=\{[z_0,z_1,\ldots, z_6]\in \mathbb {P}^6\mid z_1z_2=z_0^2, z_3z_4=z_0^2,z_5z_6=z_0^2\}$
; -
(iii)
 $D(X_6)=\{[z_0,z_1,\ldots, z_8]\in \mathbb {P}^8\mid z_1z_4=z_2z_5=z_3z_6=z_0^2z_2z_4=z_3z_0,z_7z_8=z_0^2\}$
;
$D(X_6)=\{[z_0,z_1,\ldots, z_8]\in \mathbb {P}^8\mid z_1z_4=z_2z_5=z_3z_6=z_0^2z_2z_4=z_3z_0,z_7z_8=z_0^2\}$
; -
(iv)
 $D(X_8)=\{[z_0,z_1,\ldots, z_{10}]\in \mathbb {P}^{10}\mid z_rz_{r+4}=z_0^2, \text { where }r=1,2,3,4; z_1z_3=z_2z_0, z_3z_5=z_4z_0,z_9z_{10}=z_0^2\}$
; and
$D(X_8)=\{[z_0,z_1,\ldots, z_{10}]\in \mathbb {P}^{10}\mid z_rz_{r+4}=z_0^2, \text { where }r=1,2,3,4; z_1z_3=z_2z_0, z_3z_5=z_4z_0,z_9z_{10}=z_0^2\}$
; and
-
(v)
 $D(X_9)=\{[z_0,z_1,\ldots, z_{11}]\in \mathbb {P}^{11}\mid z_rz_{r+3}z_{r+6}=z_0^3,\text { where } r=1,2,3; z_1z_3=z_2^2, z_2z_4=z_3^2, z_2z_6=z_0^2,z_3z_7=z_0^2,z_{10}z_{11}=z_0^2\}$
.
$D(X_9)=\{[z_0,z_1,\ldots, z_{11}]\in \mathbb {P}^{11}\mid z_rz_{r+3}z_{r+6}=z_0^3,\text { where } r=1,2,3; z_1z_3=z_2^2, z_2z_4=z_3^2, z_2z_6=z_0^2,z_3z_7=z_0^2,z_{10}z_{11}=z_0^2\}$
.
Example A.5.
Let
![]() $P_{X_i}$
be the polytope of
$P_{X_i}$
be the polytope of
![]() $X_i$
. For each
$X_i$
. For each
![]() $i$
, the toric variety corresponding to
$i$
, the toric variety corresponding to
![]() $P_{X_i}\times [-1,1]$
is
$P_{X_i}\times [-1,1]$
is
![]() $X_i\times \mathbb {P}^1$
.
$X_i\times \mathbb {P}^1$
.
Example A.6.
-
(i)
 $P_1=\textrm{conv}\{(\pm 1, 0, 0), (0,\pm 1, 0), (0, 0, \pm 1), (-1,-1,-1),(1,1,1)\},$
which is
$P_1=\textrm{conv}\{(\pm 1, 0, 0), (0,\pm 1, 0), (0, 0, \pm 1), (-1,-1,-1),(1,1,1)\},$
which is
 $D(X_4)$
glue with two standard 3-simplices, which the faces are all standard 2-simplices;
$D(X_4)$
glue with two standard 3-simplices, which the faces are all standard 2-simplices;
-
(ii)
 $P_2=\textrm{conv}\{ (\pm 1,0, 0),(0, \pm 1, 0), (\pm 1, \mp 1, 0), (0, 0, \pm 1), (\pm 1, 0, \mp 1), (0, \pm 1, \mp 1)\}$
;
$P_2=\textrm{conv}\{ (\pm 1,0, 0),(0, \pm 1, 0), (\pm 1, \mp 1, 0), (0, 0, \pm 1), (\pm 1, 0, \mp 1), (0, \pm 1, \mp 1)\}$
; -
(iii)
 $P_3$
, which is given by the convex hull of the points
which is a rhombic dodecahedron.
$P_3$
, which is given by the convex hull of the points
which is a rhombic dodecahedron. \begin{gather*}(1,0,0),(1,1,0),(0,1,0),(-1,0,0),(-1,-1,0), (0,-1,0), \\(0,0,1),(1,0,1),(1,1,1), (0,1,1), (0,0,-1),(-1,0,-1),(-1,-1,-1), (0,-1,-1), \end{gather*}
\begin{gather*}(1,0,0),(1,1,0),(0,1,0),(-1,0,0),(-1,-1,0), (0,-1,0), \\(0,0,1),(1,0,1),(1,1,1), (0,1,1), (0,0,-1),(-1,0,-1),(-1,-1,-1), (0,-1,-1), \end{gather*}
The subvarieties are given by the following:
-
(i)
 $P_1=\overline {\{[z_0,z_1,\ldots, z_8]\in ({\mathbb {C}}^*)^8\subset \mathbb {P}^8\mid z_1z_2=z_0^2, z_3z_4=z_0^2,z_5z_6=z_0^2,z_7z_8=z_0^2, z_1z_3z_5=z_7z_0^2\}}$
, where the last equation is deduced from
$P_1=\overline {\{[z_0,z_1,\ldots, z_8]\in ({\mathbb {C}}^*)^8\subset \mathbb {P}^8\mid z_1z_2=z_0^2, z_3z_4=z_0^2,z_5z_6=z_0^2,z_7z_8=z_0^2, z_1z_3z_5=z_7z_0^2\}}$
, where the last equation is deduced from
 $e_1+e_2+e_3=(1,1,1)$
;
$e_1+e_2+e_3=(1,1,1)$
; -
(ii)
 $P_2$
is a subvariety of
$P_2$
is a subvariety of
 $\mathbb {P}^{12}$
, so we need nine equations:
$\mathbb {P}^{12}$
, so we need nine equations:
 $z_{2r-1}z_{2r}=z_0^2$
for
$z_{2r-1}z_{2r}=z_0^2$
for
 $r=1,\ldots, 6$
,
$r=1,\ldots, 6$
,
 $z_1z_4=z_5z_0$
,
$z_1z_4=z_5z_0$
,
 $z_7z_9=z_1z_0$
and
$z_7z_9=z_1z_0$
and
 $z_7z_{11}=z_3z_0$
;
$z_7z_{11}=z_3z_0$
; -
(iii)
 $P_3$
is a subvariety of
$P_3$
is a subvariety of
 $\mathbb {P}^{14}$
. Following the order above, we have
$\mathbb {P}^{14}$
. Following the order above, we have
 $z_1z_4=z_2z_5=z_3=z_6=z_0^2$
,
$z_1z_4=z_2z_5=z_3=z_6=z_0^2$
,
 $z_1z_3=z_2z_0$
,
$z_1z_3=z_2z_0$
,
 $z_7z_9=z_8z_{10}$
,
$z_7z_9=z_8z_{10}$
,
 $z_{11}z_{13}=z_{12}z_{14}$
,
$z_{11}z_{13}=z_{12}z_{14}$
,
 $z_7z_{11}=z_8z_{12}=z_{9}z_{13}=z_{10}z_{14}=z_0^2$
and
$z_7z_{11}=z_8z_{12}=z_{9}z_{13}=z_{10}z_{14}=z_0^2$
and
 $z_8z_{11}=z_0z_1$
.
$z_8z_{11}=z_0z_1$
.
Acknowledgements
The author would like to thank Universidad autónoma de Madrid (UAM), Instituto de Ciencias Matemáticas (ICMAT) and L’Institut Montpelliérain Alexander Grothendieck (IMAG) for providing an excellent environment for the author to focus on research. The author is also very grateful to his post-doc advisors Thibaut Delcroix and Mario Garcia-Fernandez, and their post-doc and students for many fruitful discussions and advice. Moreover, the author would like to express his deepest gratitude to Jacob Sturm and Xiaowei Wang for introducing the author to the topic of Chow stabilities on toric surfaces, as well as for their very helpful suggestions, valuable guidance and encouragement. Furthermore, the author is deeply grateful to the anonymous referees for their constructive advice. Last but not least, the author is very thankful to his classmates from the Chinese University of Hong Kong for their enthusiastic discussions and advice.
Financial Support
The author is supported by grant no. EUR2020-112265 funded by MCIN/AEI/10.13039/501100011033, by the European Union NextGenerationEU/PRTR project, grant no. CEX2019-000904-S funded by MCIN/AEI/10.13039/501100011033, and by the ANR-21-CE40-0011 JCJC project MARGE.
Conflicts of Interest
None
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.





















